Deriving the Four Principles of Quantum Relativity from the Complex Temporal Dynamics of the Duality of Time Theory

Preprint � October 2025

DOI: 10.13140/RG.2.2.22599.76961

Deriving the Four Principles of Quantum Relativity from the Complex Temporal Dynamics of the Duality

of Time Theory

Mohamed Haj Yousef

Physics Department, United Arab Emirates University

mhajyousef@uaeu.ac.ae

Abstract

We propose a novel framework for quantum gravity based on a genuinelycomplex �time-time� geometry, wherein spatial dimensions emerge dynamically from sequential layers of real (inner) time, while physical evolution unfolds along an orthogonal imaginary (outer) time. This dual-temporal structure yields a hyperbolic space-time manifold that reduces to General Relativity in the appropriate limit but also provides a deeper ontological basis for discreteness, causality, and mass�energy relations.

From this framework, we derive the four foundational principles of relativistic physics�constancy of the speed of light, Lorentz transformations, the mass�energy equivalence, and the equivalence of inertial and gravitational mass�without assuming a background spacetime or external fields. The physical vacuum, reinterpreted as a dynamically re-created medium, offers a potential resolution to the cosmological constant problem and opens new insights into mass generation and quantum nonlocality.

The theory predicts several observable consequences, including gravitational wave dispersion, anomalies in the cosmic microwave background, and a fractal-like vacuum energy structure. This formulation, which we term Quantum Relativity, offers a mathematically rigorous and ontologically unified approach to quantum gravity, bridging quantum mechanics and general relativity through a discrete, emergent geometry of time.

PACS numbers: 04.60.-m, 04.20.Cv, 04.50.Kd, 03.65.Ta, 98.80.Qc

Keywords: Quantum Gravity, Emergent Space-Time, Complex-Time Geometry, Lorentz Invariance, Mass-Energy Equivalence, Cosmological Constant Problem, Vacuum Structure

Contents

1      Introduction: The Need for a Complex-Time Framework 4

2      Foundations of the Duality of Time Theory and Its Physical Implica-

���������������� tions��������������������������������������������������������������������������������������������������������������������������������������������� 5

2.1       The Duality-of-Time Postulate (DoT) . . . . . . . . . . . . . . . . . . . .��� 5

2.2       The Complex-Time Structure . . . . . . . . . . . . . . . . . . . . . . . .����������� 5

2.3       Physics from Metaphysics: the Single Monad Model (SSM) . . . . . . . .�������������� 6

2.4       Physical and Cosmological Implications of Inner-Time Dynamics . . . . .������ 7

3      Comparative Analysis with Existing Quantum Gravity Approaches�������� 9

3.1       Comparison with String Theory . . . . . . . . . . . . . . . . . . . . . . .������� 9

3.2       Comparison with Loop Quantum Gravity . . . . . . . . . . . . . . . . . .������������� 10

3.3       Comparison with Causal Set Theory (CST) and Causal Dynamical Trian-

���������������������������� gulations (CDT)������������������������������� . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .�������� 10

3.4       Comparison with Entanglement-Based Emergence Models . . . . . . . . .���������� 11

3.5       Summary and Conceptual Distinctions of DTT����������� . . . . . . . . . . . . . . 11

4      Hyperbolic Complex-Time Geometry: Mathematical Construction���������� 12

4.1       The Ontological Process Underlying the Imaginary Nature of Time������������� . . .��� 12

4.2       The Advantages of the Hyperbolic Complex-Time Frame . . . . . . . . .� 14

4.3       Discreteness and the Two Primordial States . . . . . . . . . . . . . . . .����������� 15

4.4       Supersymmetry and the Two Arrows of Time������������ . . . . . . . . . . . . . . .������������� 16

4.5       Reviving the Aether Concept and Reinterpretation Vacuum Energy . . .������ 18

4.6       Yang-Mills Conjecture and the Origin of Mass and Charges . . . . . . . .������������� 19

5      Deriving the Principles of Quantum Relativity from the DoT Postulate 20

5.1       The Constancy and Invariance of the Speed of Light . . . . . . . . . . . .���� 20

5.2       Deriving the Fundamental Invariance from Temporal Symmetry . . . . .������� 21

5.3       The Pseudo-Riemannian Limit of DTT Discrete Symmetry . . . . . . . .�������������� 21

6      Mathematical Formulation of Complex�Time Geometry�� 23

6.1       Deriving Lorentz Transformations . . . . . . . . . . . . . . . . . . . . . .���� 23

6.2       The Mass�Energy Equivalence Relation . . . . . . . . . . . . . . . . . . .�������������� 24

6.2.1       The Classical Kinetic Energy (in Normal Time) . . . . . . . . . .�������������� 26

6.2.2       Method I (Abrupt Change of Speed in the Inner Time) . . . . . .�������� 27

6.2.3       Method II (Generating Mass in the Inner Time) . . . . . . . . . .������������� 28

6.2.4       Note I (Relativistic Mass) . . . . . . . . . . . . . . . . . . . . . .���� 28

6.2.5       Note II (Mass-Energy Duality)���������� . . . . . . . . . . . . . . . . . . .����� 28

6.2.6       Note III (Effective Mass) . . . . . . . . . . . . . . . . . . . . . . .��� 29

6.2.7       Method III (Total Relativistic Energy) . . . . . . . . . . . . . . .�������� 29

6.2.8       Method IV (Complex Momentum and Energy-Momentum Relation) 30

6.3       The Equivalence Principle of General Relativity . . . . . . . . . . . . . .�������� 30

6.4       Deriving the Einstein Field Equations from the DoT Postulate . . . . . .����������� 32

 

7      Emergence of Einstein Field Equations from Inner-Time Dynamics������ 33

7.1       Statistical Structure of Emergent Geometry� . . . . . . . . . . . . . . . .����������� 34

7.2       Stress-Energy Tensor from Re-Creation Fluctuations����������� . . . . . . . . . . .������� 34

7.3       Emergent Curvature from Re-Creation Inhomogeneities . . . . . . . . . .������������� 34

7.4       Emergent Einstein Field Equations . . . . . . . . . . . . . . . . . . . . .���� 34

7.5       Complex Energy and the Fundamental Atomic Interactions . . . . . . . .������������ 35

8      Empirical Predictions and Observational Signatures�������� 36

8.1       Potential Observational Signatures of Complex-Time Geometry����� . . . . .����� 36

8.2       Quantitative Estimate: Gravitational Wave Dispersion��������� . . . . . . . . . .��������� 37

8.3       The Physical Vacuum as Dynamic Aether������� . . . . . . . . . . . . . . . . .��������� 37

8.4       Vacuum Energy and the Cosmological Constant Problem . . . . . . . . . 38

8.5       Dark Energy as a Residual Temporal Ground State . . . . . . . . . . . .������� 38

8.6       Mass Generation Without the Higgs Mechanism . . . . . . . . . . . . . .������� 38

8.7       Matter�Antimatter Asymmetry and Supersymmetry Breaking . . . . . .��������� 38

8.8       Phenomenological Predictions and Experimental Signatures . . . . . . . .�������� 39

8.9       Proposed Simulations and Experimental Tests . . . . . . . . . . . . . . .�������� 39

8.10   Future Detection Channels . . . . . . . . . . . . . . . . . . . . . . . . . .����������� 40

9      Conclusion and Outlook������������ 40

1           Introduction: The Need for a Complex-Time Framework

Modern physics rests on two foundational frameworks: General Relativity, which describes gravity as the curvature of a smooth space-time manifold, and Quantum Mechanics, which models matter and fields as discrete quanta evolving on a continuous background. Despite their empirical successes, these frameworks are fundamentally incompatible in extreme regimes, such as near black holes or the Big Bang. This tension is epitomized by the cosmological constant problem, often described as �the worst theoretical prediction in the history of physics� [1].

Numerous approaches, including String Theory, Loop Quantum Gravity (LQG), Causal

Set Theory (CST), Causal Dynamical Triangulations (CDT), Group Field Theory, and Spin Foam Models, have sought to reconcile these paradigms. Yet all presuppose some form of geometric structure�whether continuous or discrete�and none has succeeded in producing a complete and consistent theory of quantum gravity [2�8].

We argue that any successful unification must abandon the assumption of either a pre-existing continuity or discreteness of space-time. Instead, these mutually exclusive features must themselves emerge from a deeper metaphysical unity. At the level of multiplicity, entities must appear either discrete or continuous�there is no third alternative. Yet at the level of metaphysical oneness, this dichotomy dissolves. A truly foundational theory must therefore explain how the apparent duality of continuity and discreteness arises from a single, indivisible substrate. This perspective aligns with recent efforts to reconstruct space-time from quantum mechanical postulates [9], emphasizing the need to root physical geometry in a deeper underlying reality.

The Single Monad Model (SMM) [10] and the Duality of Time Theory (DTT) [11] address this challenge by positing a genuinely-complex temporal framework with two orthogonal levels: an inner, real time, in which physical dimensions are sequentially recreated, and an outer, imaginary time, along which they appear to evolve continuously. Embedded within the physical level, observers do not experience the ongoing discrete internal re-creation. Rather, they only perceive the smooth progression in the outer flow, giving rise to the illusion of continuity.

Unlike LQG, which quantizes geometry via spin networks on a fixed background [12], DTT derives geometry dynamically from inner-time processes. Space becomes a dynamically formed, multi-fractal structure, where the local dimensionality depends on the ratio between inner and outer times. In this view, the vacuum is not empty mathematical state but a structured medium, and matter particles are interpreted as its excited states. This naturally explains the emergence of mass, as well as dark matter and dark energy, as elaborated in Sections 4.6 and 4.5. Furthermore, this mechanism offers a potential resolution to the Yang�Mills existence and mass gap problem, as discussed in Section 4.6.

In addition to explaining inertia and mass, the intrinsic time-lag between re-created geometrical nodes allows the derivation of Lorentz invariance, the mass�energy relation, and the equivalence principle directly from classical mechanics�without assuming any pre-existing metric structure. As shown in Section 5, all the principles of relativity emerge naturally from the Duality of Time postulate.

Moreover, the re-creation mechanism leads to deeper physical and philosophical consequences. As demonstrated in Section 5.1, the speed of light is reinterpreted not as distance per time but as the ratio of inner to outer times�a unitless, invariant constant, equivalent to the �refresh rate� of re-creation. This new interpretation clarifies the interconvertibility of space and time observed in Special Relativity.

Finally, nonlocal correlations in quantum systems�such as those observed in the EPR paradox�are naturally accounted for in DTT, as all quantum states are synchronized at the inner levels before manifesting externally. Similarly, the large-scale homogeneity of the cosmos, usually attributed to inflation, finds a more fundamental explanation through the synchronized re-creation of all spatial regions.

Ultimately, the SMM and DTT framework unifies the continuous and discrete aspects of physical reality as complementary projections of a deeper metaphysical unity. This resolves the longstanding discreteness�continuity divide in physics and philosophy, reinterpreting General Relativity and Quantum Mechanics as effective limits of a deeper temporal process governed by a genuinely-complex time-time geometry.

By bridging foundational metaphysical insights with realistic physical modeling and rigorous mathematical formalism, DTT derives the entire structure of physical reality from a unified origin, realized through discrete complex-time dynamics. At the most fundamental level, existence is inherently discrete and unified, eliminating the need for complex calculus. Differential and tensorial mathematics only become necessary when the intricate inner dynamics of re-creation are neglected and the system is approximated by a smooth continuous manifold. In this way, DTT achieves a profound ontological simplification, while recovering the mathematical machinery of conventional physics as an emergent, limiting case. This structural inversion�deriving physical complexity from primal simplicity�marks a conceptual breakthrough, opening new avenues for unifying quantum mechanics, gravity, and cosmology within a single coherent framework.

2           Foundations of the Duality of Time Theory and Its Physical Implications

As noted above, the Duality-of-Time hypothesis and the associated concept of the dynamic emergence of spatial dimensions originate from the Single Monad Model. This cosmological framework is grounded in the metaphysical and ontological principles articulated by Muhyiddin Ibn al-Arabi, whose distinctive conceptions of time and creation diverge significantly from the traditional notions.

2.1          The Duality-of-Time Postulate (DoT)

For the purposes of this article, the core idea of the SSM and DTT can be summarized into the following postulate:

At every instance of the outer (imaginary) level of time, the spatial dimensions are continuously re-created through a precise chronological sequence of inner (real) time layers, forming nested temporal hierarchies embedded within each lower dimension.

2.2          The Complex-Time Structure

According to the above postulate, time possesses a genuinely-complex structure composed of two distinct components: an inner (real) level t_r and an outer (imaginary) level t_i. Spatial frames are discretely generated in a sequential process along the real temporal axis t_r, prior to their ordered unfolding along the imaginary axis t_i, which governs the observable evolution of physical phenomena.

The total complex time is formally defined as:

�������������������������������������������������������������������������������������������� t_c = t_r + jt_i,���������������������������������������������������� (1)

where j is the hyperbolic unit satisfying j² = +1, in accordance with the algebra of splitcomplex (hyperbolic) numbers. This hyper-complex time-time geometry is schematically illustrated in Figure 1 in Section 4, where a detailed mathematical exposition of the dynamic formation of spatial dimensions is provided.

However, the framework permits at least seven hierarchical levels of time, which dynamically intertwine to generate the ordinary space-time geometry, comprising three spatial and one temporal dimensions: (3D + T). Specifically, each of the three spatial dimensions emerges from a unique pairing among the six inner temporal cycles, while the seventh corresponds to the outer, conventional time that structures our macroscopic and perceptual experience. This septenary structure echoes the mystical symbolism of creation in six-days, also alluding a profound ontological basis for traditional time cycles, such as the Week. This pairing and subsequent breaking also forms the bases of understanding supersmmetry, as we shall explain in Section 4.4.

2.3          Physics from Metaphysics: the Single Monad Model (SSM)

This DoT postulate implies that the entire cosmos is dynamically generated through the perpetual recurrence of a single metaphysical entity operating within the real, inner layers of time. This re-creative process unfolds in a continuous temporal sequence, producing one fundamental geometrical unit at each real instant. As a result, the spatial dimensions emerge as successive temporal states, and only become manifest on the physical level through their projection into the outer layer of time perceived by observers.

As for this creative entity that is generating each fundamental geometrical unit; the Single Monad�while possessing an intricate composition that has been thoroughly examined in the cited references, it suffices to conceptualize it here, for the current discussion, analogously to the singularity at the core of a black hole: possessing zero volume, infinite curvature, and maximal information density. Ibn al-Arabi himself refers to it as �the Black Bead,� in contrast to the generated cosmic space-time, which he calls �the White Pearl� [13].

A systematic formulation of this model, along with its ontological foundations and implications, was first presented in the author�s doctoral dissertation [14], and further developed in subsequent works [10,11,15], which also provide extensive references to the historical and philosophical background of this cosmological framework. In the present study, however, we focus specifically on the implications for the dynamic structure of space-time and its consequences for quantum gravity, without delving into the broader ontological foundations.

A central feature that distinguishes this framework is its ability to derive the complexity of space-time and matter from an underlying metaphysical oneness. In DTT, the multiplicity of dimensions, mass, energy, and forces emerges dynamically through the sequential re-creation in inner-time cycles. Consequently, since existence at the most fundamental level is discrete and unified, complex calculus is not required at the foundation. Differential and tensorial mathematics, as used in General Relativity for example, become necessary only when the internal dynamics of re-creation are neglected and continuity is assumed. Thus, DTT achieves a profound ontological simplification, while recovering the structure of conventional physics as an emergent approximation. This inversion�deriving complexity from primal simplicity�marks a conceptual breakthrough toward unifying quantum mechanics, gravity, and cosmology.

2.4          Physical and Cosmological Implications of Inner-Time Dynamics

According to the above postulate, despite its inherently sequential nature, time may comprise multiple layers�some simple, others compound�depending on the complexity of the events and physical systems involved within the surrounding geometric structure. At the innermost level of reality, each instance of the real flow of time contains only a single, indivisible metaphysical entity�a fundamental geometrical point with zero spatial extent (0D). Physical multiplicity arises from the perpetual recurrence of this creative unit within the inner levels of time, giving rise to the three spatial dimensions as emergent temporal structures. These dimensions collectively constitute the observed 3D space, which subsequently evolves along the outer (imaginary) layer of time, producing the familiar extended manifold: 3D + T.

Since observers are themselves constituted through the same process, they do not directly perceive the ongoing re-creation, but they remain in �lapse� during this inner temporal cycle. They become �active� only at the successive discrete instants of the outer-time, when they themselves are re-created. Consequently, observers perceive a continuous and coexistent reality, mistakenly assuming that all entities persist in an unbroken state of being, when in fact they are only temporally becoming in successive indivisible instances. This fundamental lapse in perception underlies our conception of time as a �continuous extension�, rendering it �imaginary�, in contrast to space, which is perpetually re-generated through the discrete unfolding of real time. As Hawking rightfully noticed: �In fact, one could take the attitude that quantum theory, and indeed the whole of physics, is really defined in the Euclidean region and that it is simply a consequence of our perception that we interpret it in the Lorentzian regime.� [16]. The DTT provides a concrete ontological basis for this deceptive perception.

This perceptual limitation legitimizes the use of infinitesimal calculus and differential geometry, whose foundational assumptions align with this apparent continuity. These mathematical frameworks, while effective, are mere approximations that emerge from the deeper granular structure described by the above DoT postulate. In Section 5.3, we clearly show how this framework converges to General Relativity in the limit when inner-time dynamics are neglected, thus fulfilling the correspondence principle that any new theory must recover established theories under appropriate limiting conditions.

Furthermore, in Section 4.4, we demonstrate that the physical and psychical realms are governed by two orthogonal arrows of time. Observation occurs as a result of the interaction between these dual temporal dimensions, described by the hyperbolic Lorentzian symmetry, while their interplay yields a spherical Euclidean space.

Consequently, space appears symmetric and continuous (Euclidean) background because the observer imagines all its geometrical points continuously coexisting. Time, however, is perceived as discrete and imaginary�being nothing more than the illusion formed by the succession of individually refreshed instances. This aligns perfectly with the profound views of Parmenides and Zeno, who argued that motion and multiplicity are illusory [17].

As elaborated in Section 4.3, this fundamental complex-time micro-structure reduces the universe to a digital system governed by only two primordial states: existence and non-existence, or �1� and �0�, which correspond to vacuum and void, respectively. However, the �vacuum� is redefined here as the result of layered spatial emergence, which has an inner physical structure, whereas the �void� corresponds to a total absence of structure�a true mathematical vacuum.

Therefore, analogous to the operation of a digital display on a computer monitor, this framework likens the physical world to a sequence of rapidly refreshed frames, each constructed sequentially pixel-by-pixel in the two dimensions of the screen. If we were to pause the outer flow of time, we would see a static frame of spatial geometry. However, if we could halt the inner (real) time, all structure would dissolve into a singular metaphysical point, devoid of any background, apart from the imaginary mathematical space. Recent efforts to describe spacetime emergence in quantum cosmology [18] find a natural parallel in this creative vacuum.

This critical redefinition of vacuum leads to a novel revival of the aether, though in a form that does not interfere with the speed of light. Rather than existing within space, this new aether is the physical vacuum itself �the very background geometry. Unlike the traditional concept, this aether does not violate relativity, since it does not define a preferred frame. Instead, the re-creative dynamics of inner-time offer a natural ontological explanation for the constancy and invariance of the speed of light�currently postulated as an empirical axiom without theoretical derivation. This will be elaborated further in Section 4.5.

Furthermore, if empty space (as structured vacuum) is the ground state of matter, then it contributes intrinsically to the total mass�energy content of the universe. This contribution may explain the missing dark matter and energy. Additionally, because this vacuum is temporally layered, its energy density should be computed as a time-averaged ground state�not as the collective summation used in current quantum field theory approaches. This insight could resolve the long-standing vacuum catastrophe, reducing the discrepancy in the cosmological constant by over 117 orders of magnitude�a topic explored further in Section 4.5.

In the quantum realm, the sequential re-creation model offers a fresh ontological basis for the wave�particle duality, as well as essential phenomena such as uncertainty, measurement, and the observer effect. These are traditionally interpreted probabilistically but remain philosophically problematic. As Niels Bohr suggested, the wave�particle duality may be a metaphysical fact of nature [19]. In this framework, suppose a quantum particle is composed of N internal monads or oscillatory modes; at each real instance of time, only one of these modes is actively created at the speed of light, while the others have collapsed into passive states.

Therefore, since the particle�s final eigenstate becomes definite only once its last active mode collapses, the position of a particle�initially uncertain due to its light-speed internal dynamics�becomes instantly defined. The uncertainty in energy and time, expressed as ∆E ∆T ≥ ℏ/2, can now be reinterpreted: since ∆T ∝ N, it follows that ∆E ∝ 1/N. This inverse relation provides a physically intuitive explanation for the Heisenberg uncertainty principle, grounded in the temporal structure of reality. Other profound conclusions related to Quantum Mechanics, such as supersymmetry, will be discussed further in Section 4.4.

In conclusion, DTT has the potential to unify the foundational principles of relativity and quantum theories�including both the first and second quantizations, of energy and fields, and it also naturally leads to a �third quantization� of space-time itself. By treating geometry as an emergent consequence of metaphysical unity, this framework offers a pathway to eliminate the divergent infinities that afflict continuum-based models of quantum gravity.

Having introduced the Duality-of-Time postulate and outlined the sequential emergence of space-time through complex temporal layers, it is instructive to situate this framework within the broader landscape of contemporary approaches to quantum gravity. In the following Section, we compare DTT framework with several leading theories, including String Theory, Loop Quantum Gravity, and Causal Set Theory, highlighting both conceptual distinctions and complementary insights. This comparative analysis clarifies the novel contributions of DTT and underscores its potential to address longstanding challenges in reconciling the quantum and relativistic domains.

3           Comparative Analysis with Existing Quantum Gravity Approaches

The DTT introduces a fundamentally distinct framework for quantum gravity by positing that spacetime emerges dynamically through a genuinely-complex time-time geometry. Unlike most leading approaches, DTT derives both continuity and discreteness internally from temporal flows, without presupposing any fixed geometric background or external quantization procedure. In this Section, we highlight the main differences and complementarities between DTT and several major quantum gravity programs. Key distinctions of DTT include:

Time Structure: Splits time into real (generative) and imaginary (evolutionary) components, unlike conventional or relational treatments.

Vacuum Energy: Naturally resolves the cosmological constant problem via realtime averaging, avoiding the 10¹²⁰ discrepancy without fine-tuning.

Lorentz Invariance: Lorentz symmetry arises inherently from DTT�s complextime geometry rather than being imposed.

Mass�Energy Origin: The mass-energy relation E = mc² follows intrinsically from inner-time dynamics, without external fields or symmetry breaking.

Singularity Avoidance: Continuous re-creation processes prevent singularities like the Big Bang and black holes, without requiring quantum bounces or string fuzziness.

Background Independence: Eliminates any pre-existing spacetime assumptions, achieving a deeper level of background independence than other models.

3.1          Comparison with String Theory

String Theory models fundamental particles as one-dimensional extended objects vibrating in higher-dimensional backgrounds, typically formulated within fixed smooth manifolds or supersymmetric configurations [20]. Spacetime itself remains largely pre-assumed, although emergent features arise in certain limits, such as AdS/CFT duality [21].

By contrast, in DTT, the very existence of spatial dimensions and metric structure arises dynamically from sequential layers of inner (real) time. No pre-existing higherdimensional manifold is required, and the emergence of spacetime is inseparable from the metaphysical foundation of temporal re-creation. While String Theory emphasizes unification via extended objects, DTT emphasizes unification via the dynamic formation of space and matter from the dual flow of complex time.

Although String Theory aims to unify all interactions, it depends on supersymmetry and compactified dimensions [2,3]. DTT challenges this by deriving dimensionality from inner temporal cycles alone. Supersymmetry, in this view, arises from the alternation between real and imaginary time axes.

Moreover, the cosmological constant problem remains unresolved within String Theory due to the large vacuum energy contributions from zero-point modes [22]. By contrast, DTT redefines vacuum energy as a temporal average across re-created states, rather than their collective summation, significantly reducing the expected vacuum energy and resolving the discrepancy without fine-tuning.

3.2          Comparison with Loop Quantum Gravity

LQG seeks a non-perturbative quantization of General Relativity by discretizing geometry through spin networks and spin foams, preserving background independence at the level of kinematical states [4]. LQG quantizes the spatial geometry but still relies on a continuum manifold as an underlying structure [5].

In contrast, DTT does not quantize a pre-existing space. Rather, the space itself is a dynamically emergent structure resulting from the discrete real-time re-creation of geometrical nodes. Furthermore, while LQG uses external combinatorial graphs to encode quantum states, DTT derives spatial discreteness directly from inner time layering, with motion and causality arising from the orthogonal imaginary time flow.

Furthermore, LQG constructs quantum geometry via a canonical Hamiltonian formalism [23,24]. In contrast, DTT derives relativistic dynamics directly from the inner mechanics of temporal layering, yielding exact Lorentz transformations and mass-energy equivalence from a first-principles process of temporal discretization.

3.3          Comparison with Causal Set Theory (CST) and Causal Dynamical Triangulations (CDT)

CST and CDT model spacetime as a discrete set of events ordered causally. These approaches emphasize the fundamental discreteness of spacetime while preserving Lorentz invariance statistically [25]. CST introduces discreteness externally as posets [6], and spacetime volume emerges from the cardinality of the set, while CDT reconstructs geometry through dynamically triangulated simplices constrained by causal order and local Lorentz invariance. Both retain discreteness as a central feature. The DTT aligns with this in asserting a fundamentally discrete substrate, yet its causal structure arises from the ordered succession of re-creation events, not imposed externally. It offers a more deterministic foundation, with geometric and physical properties derived from the inherent sequencing of temporal events.

Glaser and Surya [26] discuss the cosmological potential of causal sets, which could be complemented by DTT�s fractal vacuum dynamics. While it provides a discrete and covariant foundation, CST lacks a mechanism for generating dynamics or recovering continuum physics with precision. DTT similarly adopts a discrete structure but introduces an inherent sequential generative process through metaphysical time. This allows for natural emergence of causality and dimensionality without random sprinkling. [27,28]

DTT shares with these approaches the fundamental idea that spacetime is discrete at a deep level, but it also explains the origin of causal structure dynamically: causality and spatial adjacency emerge from the nested temporal generation of geometrical points, rather than being postulated axiomatically. Unlike CST, which postulates causality via discrete posets [29], DTT derives it from temporal re-creation. Recent work shows that causal set dynamics can suppress non-manifold-like configurations, reinforcing the idea that discrete structures can robustly recover continuum spacetime without fine-tuning [30]. Moreover, DTT accommodates both the discrete and continuous limits naturally through the dual levels of inner (real) and outer (imaginary) time, recovering smooth pseudo-Riemannian geometry when inner dynamics are averaged out (see Section 5.3).

3.4          Comparison with Entanglement-Based Emergence Models

Recent developments propose that spacetime geometry emerges from quantum entanglement patterns, particularly in the context of holographic principles such as the AdS/CFT correspondence [31,32], entanglement entropy [33] and tensor network models like MERA [34]. In these frameworks, the structure of spacetime is encoded in the entanglement entropy of underlying quantum degrees of freedom.

DTT offers a complementary but more foundational perspective: the emergence of spatial dimensions, mass, and energy results from the metaphysical re-creation of geometrical structures in complex-time, prior to any conventional quantum state entanglement. Entanglement in DTT arises as a consequence of the synchronized internal creation processes, rather than being the primary source of spacetime geometry. Moreover, proposals for tabletop quantum experiments targeting emergent spacetime phenomena highlight a growing interest in empirical detection of quantum-geometric structures [35]. Thus, DTT proposes a pre-quantum origin for the fabric of spacetime, where quantum phenomena are secondary manifestations.

3.5          Summary and Conceptual Distinctions of DTT

In this light, DTT may serve not only as an alternative foundation for quantum gravity, but also as a conceptual meta-framework within which other models might be interpreted, extended, or unified. Table 1 summarizes the key conceptual differences between DTT and other leading quantum gravity frameworks.

Thus, DTT offers a novel route toward unifying quantum mechanics and gravitation, by grounding physical reality in a metaphysical temporal structure that dynamically generates space, matter, and motion. This conceptual foundation not only reconciles continuity and discreteness but also provides new avenues for empirical investigation, as outlined in Section 8.

Table 1: Comparison between DTT and Existing Quantum Gravity Approaches

Feature	SMM and DTT	LQG������� /����� CST���� / CDT	String Theory / AdS/CFT
Origin���������� of Spacetime	Emergent from complex-time dynamics (no pre- assumed structure)	Discrete elements on fixed or statistical background	Smooth manifold or boundary assumed; emergent features at limits
Continuity vs Discreteness	Both arise dynamically from dual temporal flows	Discreteness fundamental; continuity emergent statisti- cally	Continuity fundamental; discreteness secondary
Background Independence	Full:����� no�������������� presupposed geometry	Partial: discrete structure built over assumed continuum	Partial: background needed for dualities
Causality	Emergent from sequential real-time generation	Postulated causal relations	Emergent in specific holographic models
Role�������������� of Quantum Entanglement	Secondary to inner temporal re-creation	Not primary	Primary (geometry from entanglement)
Mass������ Gen- eration	Dynamic re-creation through structured vacuum; no Higgs required	Largely unexplained; external fields or boundary conditions	Via������� symmetry breaking (e.g., Higgs mechanism)

4           Hyperbolic Complex-Time Geometry: Mathematical Construction

According to the DoT postulate outlined above, we can illustrate the genuinely-complex time-time geometry schematically in Figure 1, where space is represented in two dimensions (x,y), with the dynamics simplified to focus on the x -axis, for simplicity.

4.1          The Ontological Process Underlying the Imaginary Nature of Time

The concept of imaginary time already plays a pivotal role in various mathematical formulations within quantum physics and cosmology, although often as a computational device rather than a physically motivated construct. As Hawking observed: �It turns out that a mathematical model involving imaginary time predicts not only effects we have already observed, but also effects we have not been able to measure, yet nevertheless believe in for other reasons.� [36].

In conventional treatments, imaginary time is typically introduced as a dimension orthogonal to the ordinary time, coexisting with space. However, under the DoT, the picture is reversed: space is dynamically generated in the real flow of time, while the normal (observable) time becomes genuinely imaginary, or latent�a projection of the

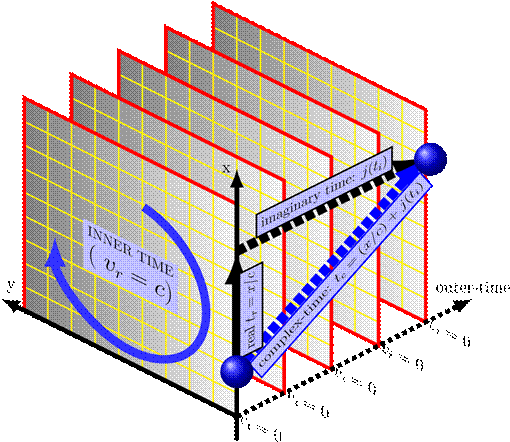
Figure 1: Representing the inner and outer levels of time together as genuinely-complex time-time geometry. The discrete frames of space are internally generated within the real flow of time t_r, and then they unfold sequentially along the imaginary level t_i, making the total complex-time: t_c = t_r + jt_i.

inner generative flow.

As demonstrated in Figure 1, whenever the real flow is interrupted, a new orthogonal dimension emerges. This transition is mathematically realized through multiplication by the imaginary unit: j, effecting an abrupt rotation by π/2. This subtle property introduces the essential discreteness of space-time as a direct consequence of the dual nature of time, which flows either inwardly (real) or outwardly (imaginary), but not both simultaneously. As a result, the emergent space-time geometry is inherently fractal and genuinely-complex, comprising real and imaginary components. If, on the other hand, all dimensions were assumed to coexist simultaneously within a single real-time instance, space would appear smooth and continuous, as commonly imagined. However, such an deceptive assumption leads to inconsistencies and singularities under extreme physical conditions.

Therefore, this framework naturally accommodates the use of imaginary time to connect quantum mechanics with statistical mechanics via Wick rotation (a π/2 rotation in the complex-time plane). This technique enables reformulation of dynamical problems in n dimensions into equivalent problems in n + 1 dimensions by trading one spatial coordinate for a temporal one. Notably, the Schro�dinger and heat equations are related in this way. Wick rotation also underlies Feynman�s path integral formalism, which was extended in 1966 by DeWitt into a gauge-invariant functional-integral approach [37].

Motivated by these connections, numerous efforts have been made to describe quantum gravity using Euclidean geometry [16,38]. This approach allows for the avoidance of spacetime singularities that arise in General Relativity, which is constructed on a Riemannian manifold whose geometry becomes ill-defined in extreme regimes.

4.2          The Advantages of the Hyperbolic Complex-Time Frame

In the DoT framework, ordinary time is interpreted as a genuinely imaginary and fractional dimension, in contrast to the spatial dimensions, which are dynamically generated as complete and integer-valued spatial dimensions through the real flow of inner-time. When isolated from any dynamic activity, the resulting spatial axes are spherically orthogonal, consistent with the isotropic and homogeneous structure of Euclidean space. This configuration can be modeled using standard complex numbers C, with the modu-

lus given by |z| = ^px² + y². Split-complex geometry offers an alternative foundation for relativity transformations [39].

By contrast, the outer (imaginary) time dimension is incomplete and non-integer, and is therefore hyperbolically orthogonal to space. This is best described using the algebra of split-complex numbers (also known as tessarines, perplex numbers, bi-real, semicomplex, or motors), denoted here as H ≡ R(j). In this algebra, the modulus is defined

as ∥z∥ = ^px² − y². Unless otherwise stated, the terms imaginary and complex in this paper refer specifically to these split-complex numbers.

Accordingly, the complex-time is expressed as t_c = t_r + jt_i, where the real part t_r =

^pt²_x + t²_y + t²_z = ^p(x/c)² + (y/c)² + (z/c)² is associated with spatial dimensionality, and t_i represents the imaginary part, corresponding to the outward or observed temporal flow.

The negative sign in the split-complex modulus ∥t_c∥ = ^pt²_r − t²_i reflects a central feature of the DoT model: the continuous re-creation of space via t_r is interrupted at each instance of outward (imaginary) time t_i, giving rise to observable kinetic motion. If the inner generative flow t_r were uninterrupted, the result would be a static Euclidean vacuum state�describable using R or C�represented as (t_r,0) or (c,0). Conversely, any physical object evolving outwardly in time appears as (t_r,t_i), or equivalently as (c,v).

In this abstract framework, both space and time are treated as absolute entities in a mathematical sense, akin to Newtonian mechanics. However, the concept of void is now explicitly distinguished from that of the physical vacuum. The void (0,0) denotes a pure mathematical state with no physical content or metaphysical activity, while the vacuum (t_r,0) corresponds to a physically real but inert ground state, continuously re-created at the speed of light c. A moving object is thus characterized by the pair (t_r,t_i), signifying that it is re-created internally at the intrinsic speed c, and observed externally at the apparent velocity v.

The idea of imaginary time was first introduced in early relativistic physics by Poincar�e [40] and later formalized by Minkowski [41]. However, in the absence of any physical interpretation for imaginary time, Minkowski reformulated space-time as a four-dimensional pseudo-Euclidean manifold (x,y,z,t) with Lorentzian signature (+,+,+,−), treating time as a fourth coordinate with a negative sign. This formalism became a cornerstone of General Relativity, which requires Riemannian geometry to accommodate gravitational curvature.

In contrast, the hyperbolic geometry of split-complex numbers provides an alternative foundation for relativity, allowing Lorentz transformations to be interpreted as rotations in the imaginary (hyperbolic) plane [42]. Within this framework, the discrete symmetry of complex-time implies that the instantaneous velocity along the imaginary axis is always zero (cf. Fig. 1), regardless of acceleration. As a result, Lorentz transformations apply equally to inertial and non-inertial frames. Moreover, this intrinsic symmetry enables a direct derivation of the equivalence principle that underlies General Relativity�a topic addressed in Sections 6.1 and 6.2.

4.3          Discreteness and the Two Primordial States

As illustrated in Figure 1 and detailed further below in Section 4.2, one of the most profound consequences of the sequential re-creation process is the emergence of only two primordial states: vacuum and void. The first is denoted as (c,c), which corresponds to continuous existence in the real levels of time, while void is denoted as (0,0), representing the discontinuous imaginary time. All observable phenomena arise from the superposition of these two states. This binary structure parallels ontological minimalism in recent discussions of quantum subsystems, where emergent properties arise from spectral characteristics of more primitive states [43].

Therefore, the instantaneous velocity v_i in the outer (observable) time is identically zero, regardless of whether the object is stationary or in motion (uniform or accelerated). Conversely, though fundamentally indefinite rather than infinite, the intrinsic speed v_r in the inner-time is effectively equal to the speed of light c, which is also identical with the refresh-rate of re-creation. Since it is originally initiated at the metaphysical level of absolute oneness, where no temporal or spatial extensions can be perceived. Nevertheless, the finite speed c is the result of the time-lag experienced by observers, during which the spatial dimensions are re-created. Consequently, the observed physical velocity v emerges as a dynamic combination of these two extremes, as defined by Equation 2 in Section 4.3.

Nevertheless, it is crucial to recognize that, despite its complex multilayered structure, time remains fundamentally a single, sequential order. This implies that no two events can occur at the same real instant, and no two entities can simultaneously exist in an active state. As a result, the instantaneous velocity v_i in the outer (observable) time is identically zero, whether the object appears stationary or in uniform or accelerated motion. Conversely, the intrinsic speed v_r within the inner-time�though fundamentally indefinite rather than infinite�is effectively equal to the speed of light c, corresponding to the refresh rate of re-creation. The finite value of c arises from the time-lag experienced by observers, during which the spatial dimensions are sequentially re-created.

This re-creative process originates at the metaphysical level of absolute oneness, where neither temporal nor spatial extensions are perceivable. Continuous real-time flow gives rise to homogeneous vacuum states: (c,c), while any disturbance introduces discrete void events: (0,0). The interplay between these dual states generates complex dynamics that are perceived as motion, expressed as (c,v). Consequently, the observed physical velocity v emerges as a dynamic combination of these two extremes of the dual-state oscillations, as defined by Equation 2:

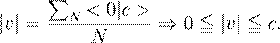��������������������������������������������������������������������� �������������������������� (2)

Each geometrical node is massless and binary (0 or c), but collectively they yield objects with inertial mass m, energy E, and finite effective velocity v. Motion, therefore, is not continuous translation, but successive re-creations at discrete positions�echoing Zeno�s �Moving Arrow� paradox [17].

In this view, the universe re-emerges �in zero time� from the imaginary-time perspective. Points oscillate between vacuum and void, with instantaneous speeds always v_imaginary = 0 or v_real = c. These abrupt transitions do not violate physical laws because they occur in the metaphysical domain prior to the formation of physical properties. In Section 6.2, we shall see how this fundamental dual-temporal structure of complex-time enables the derivation of the mass�energy equivalence relation from first principles. While already evident in photon behavior, DTT extends this re-creative mechanism to all particles, framing physical space, mass, and energy as emergent from temporally entangled, massless geometrical points.

4.4          Supersymmetry and the Two Arrows of Time

As introduced in Section 2, our perception of continuous coexistence arises from only witnessing spatial configurations after their generation in real time. The illusion of continuity thus emerges from a sequential process of re-creation. To represent this relationship, we write:

As explained in Section 4.1, discreteness emerges from the interruption of the perpetual re-creation of spatial dimensions, which introduces multiplication by the imaginary unit j, yielding a new temporal component that is hyperbolically orthogonal to the otherwise Euclidean vacuum. Repeating this mathematical transformation�equivalent to a Wick rotation by π/2�generates an additional real (spatial) direction. Consequently, every point in our observed 3D + T space-time arises from the combination of seven temporal levels: six inner real levels corresponding to the three spatial dimensions, and a seventh outer level associated with the imaginary time.

Therefore, this outer-time t_i, effectively acts as a delay or projection of the inner real temporal flow t_r, but never surpasses it, because time is a sequence being directed either inward (real) or outward (imaginary)�they cannot manifest simultaneously within a single frame of physical reality. This relationship can be formally expressed as:

�������������������������������������������������������������������������������������������� 0 ≦ t_i ≦ t_r.���������������������������������������������������� (3)

Given this inequality, the modulus of complex-time satisfies ∥t_c∥ = ^pt²_r − t²_i ≤ t_r, which corresponds to the proper time. Unlike the positive-definite modulus in Euclidean geometry, the split-complex modulus adopts a Lorentzian signature (1,−1), allowing for the reversal of roles. Specifically, in the configuration t_c = t_i +jt_r, the modulus becomes

∥t_c∥ = ^pt²_i − t²_r, implying t_r ≤ t_i from the observer�s perspective (as opposed to the normal case described by Eq. 3). In this scenario, the vacuum state is represented as (0,c), corresponding to anti-matter.

The observed velocity v is constrained by v ≤ c because it arises as an average over fluctuating instantaneous velocities of all constituent nodes, described by Eq. 2. Thus, from Eq. 3, we have: 0 ≤ |v| ≤ c, with the limiting cases: t_i → t_r = x/c implies v → c, while t_i = 0 yields v = 0. Hence, the vacuum state is characterized by (t_r,0) or equivalently (c,0)�corresponding to a flat, static, infinite Euclidean space.

In this context, the imaginary time t_i acts as a form of inertia that resists the flow of real time t_r, which gives rise to motion and generates the rest mass m₀ that increases with velocity according to the relativistic relation m = γm₀, as discussed in Sections 6.2, 4.6, and 6.2.3. As t_i → t_r, we approach the limit v → c and m → ∞. This limiting configuration, denoted by (c,c), represents a state of both real and imaginary continuity, producing a homogeneous Euclidean space of one higher spatial dimension.

Interestingly, the state (c,c) constitutes a null, non-invertible vector in the hyperbolic plane H�since |t_c| = 0�yet it represents an isotropic and inert Euclidean space when viewed from the inner temporal perspective. The Universe oscillates between this maximal, or �super-energy�, state (c,c) and the �super-fluid� vacuum state (c,0), while physical evolution occurs through the intermediate configurations (c,v), where 0 < v < c. These configurations reflect the outer (imaginary) time dynamics in H and the inner (real) spatial unfolding in C. Singularities and infinities arise precisely when these orthogonal perspectives are conflated within a single geometric framework.

As elaborated in Section 5.3, General Relativity provides an accurate local approximation of this dynamic geometry; however, its global consistency necessitates a hyperbolic reformulation. GR remains valid at each instantaneous frame, but the cumulative effects across sequential re-creation steps require a quantum field theoretic (QFT) treatment embedded in the complex-time manifold.

Consequently, the entirety of homogeneous space reduces to a single temporal point from the inner-time viewpoint, and extended space-time emerges dynamically as a continuous interplay between the two fundamental extremes: (c,0) and (c,c). In this framework, no two spatial points coexist in the same temporal instant; instead, they are sequentially re-created. Since no physical object can attain the speed of creation c, the emergence of new spatial dimensions occurs through the fusion of the orthogonal vacuum states (c,0) and (0,c)�a process naturally interpreted as matter�antimatter annihilation:

�������������������������������������������������������������������������� (c,0) + (0,c) ⇄ (c,c) + (0,0).���������������������������������� (4)

This means that the Universe is fundamentally oscillating between two primordial states: the void (0,0) and the vacuum (c,c). The latter represents a perfect Bose�Einstein condensate�a unified, undifferentiated state devoid of distinguishable particles. From this ontological unity, multiplicity emerges through a primordial symmetry breaking: the super-energy state (c,c) and the super-mass state (0,0) bifurcate into the superfluid (c,0) and the super-gas (0,c). These correspond, respectively, to particles and anti-particles, which continuously annihilate and re-emerge in a cyclical process. This dynamic constitutes the very essence of time and underlies both physical perception and conscious experience [15].

Were the Universe to remain trapped in the bosonic condensate (c,c), neither (the outer) time nor physical particles would manifest. Time begins with the excitation of the super-fluid vacuum (c,0)�interpreted as the aether�into the state (c,v), which corresponds to the emergence of matter particles. Simultaneously, its orthogonal counterpart (0,c) becomes (v,c), representing anti-matter. Each of these states behaves as a fermion within its own temporal frame, while appearing bosonic from the orthogonal perspective, owing to the dual and orthogonal structure of time inherent in the complex-time geometry.

In conclusion, the complex flow of time admits three principal regimes:

1.   Normal time: t_i < t_r, yielding (c,v) (matter in space-time).

2.   Orthogonal time: t_i > t_r, yielding (v,c) (anti-matter).

3.   Balanced time: t_i = t_r, yielding (c,c) (super-energy/vacuum).

Together with the ground mathematical void, these correspond to the four classical elements�super-mass (0,0), super-fluid (c,0), super-gas (0,c), and super-energy (c,c)�whose quintessence is the Single Monad [44].

As shown in Figure 1, the space-time interval is given by: ∥s∥ = ^[1]x² + y² + z² − (ct_i)² =

ativity but with a negative signature:

.

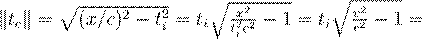
This negative signature emerges from the fact that we inhabit the imaginary temporal dimension and must accumulate successive discrete intervals to construct the perception of spatial continuity. For example, even the mental representation of a simple spatial segment requires at least three distinct temporal instances�one for each endpoint and one for their relational structure�implying that complete spatial perception demands an effectively infinite temporal sequence. Were our consciousness situated within the real (inner) spatial dimensions, space would be perceived instantaneously, much like the experience near a black hole�s event horizon, where proper time ceases. Consequently, what we conventionally interpret as �real� time is, within this framework, genuinely imaginary, while true ontological reality arises from the interplay between the inner (real) and outer (imaginary) temporal levels.

This foundational asymmetry�where outward (imaginary) time possesses a negative signature relative to real inner-time�propagates to all derived physical quantities. Velocity, momentum, and energy all inherit corresponding imaginary or negative components when referenced to their real-time analogs. This dual-temporal structure underlies the derivation of key relativistic relations, including the energy�momentum equivalence, mass transformation principles, and the multidimensional generalization of mass and energy, as will be demonstrated in Sections 6.1 and 6.2.

4.5          Reviving the Aether Concept and Reinterpretation Vacuum Energy

The notion of aether dates back to antiquity as a subtle medium pervading space. Reintroduced in the 19^th century as the �luminiferous aether� to explain light propagation, it was experimentally undermined by the Michelson-Morley experiment [45], leading to its abandonment with the rise of Special Relativity. Yet Einstein later remarked that spacetime itself could be viewed as a kind of aether, since it endowed empty space with physical properties [46].

In the 20^th century, Dirac [47] and others revisited aether-like concepts, which evolved into modern scalar field theories like quintessence [48�50], a dynamic vacuum energy candidate possibly responsible for cosmic acceleration [51].

Within DTT framework, the classical concept of aether is reinterpreted as the physical vacuum itself, functioning as an inert superfluid ground state (c,0) from which all matter states (c,v) can be excited, as explained in Section 4.4 above. When motion vanishes in both the real and imaginary time directions, the system asymptotically approaches a pure BEC state, thereby unifying quantum field theory (QFT) concepts of vacuum and scalar fields [52].

In QFT, the vacuum energy arises from the zero-point states of quantized harmonic oscillators. The Klein-Gordon field contributes infinite zero-point energy, mitigated by

introducing a cutoff at the Planck length: ℓ_P = ^pℏG/c³ ≈ 1.616 � 10⁻³⁵ m. This leads

to a Planck energy E_P = ^pℏc⁵/G ≈ 1.22 � 10¹⁹ GeV. The vacuum energy density then becomes ρ_vac = E_P⁴/(8π²ℏ³c³) ∼ 10⁷⁶ GeV⁴. In contrast, astronomical observations yield ρ_vac ∼ 10⁻²⁹ GeV⁴, leading to the infamous vacuum catastrophe, a discrepancy of 120 orders of magnitude [53�55].

According to DTT, this discrepancy is reduced�or even eliminated�by recalculating vacuum energy as an average rather than a summation of all zero-point contributions. If the Planck length is used as a cutoff, the number of independent modes in a unit volume is: 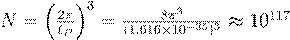. The remaining discrepancy could be explained by quintessence-like fluctuations already encoded in the model. This provides a new solution to the vacuum catastrophe, famously quantified in [56].

Moreover, the proposed fractal geometry eliminates the need for imposing an arbitrary cutoff scale, such as the Planck length, which lacks a rigorous physical justification. In this framework, neither space nor time requires discrete units or minimum quanta individually; rather, the fundamental constraint arises from their ratio�the refresh rate that is equivalent to the normalized value of the speed of light�as introduced in Section 1 and elaborated further in Section 5.1.

4.6          Yang-Mills Conjecture and the Origin of Mass and Charges

In modern physics, mass is widely regarded as an emergent property. Within the Standard Model, the Higgs mechanism accounts for particle masses through spontaneous symmetry breaking of gauge and chiral symmetries [57,58]. However, the origin of the Higgs boson�s own mass remains unexplained.

In DTT framework, the physical vacuum is modeled as a perfect superfluid, and particle masses emerge through interactions with this dynamically re-created medium�analogous to gap formation mechanisms in superconductivity [59�61]. This interpretation, rooted in the genuinely-complex time-time geometry introduced in Section 4.2, offers a more unified and natural account of mass generation.

Here, inertial mass arises from a finite time delay in the response of coupled constituents within a system. Due to the discrete nature of space-time, geometrical points do not coexist but are instead sequentially re-created. This temporal separation introduces inertia as a consequence of delayed interactions.

Consequently, any physical object must consist of at least two geometrical nodes. Their coupling defines discrete interaction parameters, such as charge and mass. A single node corresponds to a massless boson, whereas configurations involving multiple nodes acquire mass based on their internal temporal structure. Some bosons may appear massive due to confinement or emergent effects, though they remain intrinsically massless in lower-dimensional configurations.

Additionally, this structure naturally predicts a minimum mass gap above the vacuum state (c,0), with the next accessible state requiring at least two sequentially separated nodes. This prediction resonates with the Yang�Mills mass gap hypothesis, wherein internal degrees of freedom are inherently tied to space-time structure [62]. Proving this conjecture is widely believed to demand new conceptual frameworks in both physics and mathematics [63].

Thus, DTT framework offers a novel resolution to the mass gap problem by introducing a discrete, superfluid vacuum with quantized mass levels�emerging from the dynamics of complex-time geometry. This perspective aligns with recent advances in structural quantum gravity, which emphasizes mass and interaction emergence from discrete informational architectures [64].

5           Deriving the Principles of Quantum Relativity from the DoT Postulate

The Michelson-Morley experiment demonstrated that the speed of light in vacuum is invariant with respect to Earth�s motion [45], establishing c as a universal constant independent of both the source and the observer. Massless particles, such as photons, always propagate at this maximal velocity.

While this invariance is empirically well established, its theoretical origin remains elusive. No derivation from first principles fully explains why all observers measure the same light speed, regardless of relative motion.

Einstein adopted this empirical fact as a postulate of Special Relativity, extending Galilean invariance to include Lorentz transformations. He later introduced the equivalence principle to generalize the theory to non-inertial frames, equating inertial and gravitational mass via a conceptual thought experiment involving uniform acceleration. Despite their success, these postulates remain axiomatic. In standard relativity, they are not derived from deeper physical or geometrical principles.

Therefore, in its conventional form, relativity rests upon these three core principles:

Galilean Invariance (extended to Lorentz Invariance).

Constancy of the Speed of Light.

Equivalence of Inertial and Gravitational Masses.

In this section, we show how DTT provides a fundamental derivation of these principles, grounded in the dynamic formation of spatial dimensions, as introduced in Section 4. Here we shall give the ontological justification, while the derivations are formalized mathematically in Section 6.

Moreover, DTT offers a first-principles derivation of a fourth foundational principle often treated empirically: the mass�energy equivalence E = mc². While experimentally validated, this relation lacks a rigorous derivation within classical relativity [65]. We address all these derivations with overwhelming details, in Section 6.2.

Moreover, DTT provides a first-principles derivation of a fourth foundational principle often accepted empirically: the mass�energy equivalence E = mc². Although this relation is firmly supported by experimental evidence, it remains without a fully rigorous derivation within classical relativity [65]. A comprehensive treatment is presented in Section 6.2, made possible only after uncovering the discrete symmetry arising from the dynamic generation within the inner levels of time.

Together, these four principles�three reinterpreted, one newly derived�form the basis of a generalized framework we term as: Quantum Relativity, unifying relativity and quantum theory through the complex-time geometry of DTT.

5.1          The Constancy and Invariance of the Speed of Light

There are only two logical scenarios in which a quantity appears unchanged when altered: either it is infinite, or it exists within a dimension orthogonal to the modification. Such extreme behavior can only be justified within DTT, in which the speed of light is equivalent the rate of space re-creation.

This refresh rate is fundamentally indefinite, rather than infinite, since it is originating at the metaphysical level of absolute oneness. The finite speed c that is measured at the physical level arises from the sequential re-creation process, as perceived by observers embedded within it, who thus experience a time-lag during which spatial dimensions are regenerated.

Moreover, because normal time is genuinely imaginary in this framework, all physical motion occurs orthogonally to the real, infinite process of re-creation. For observers situated in imaginary time, creation appears instantaneous, as they perceive only the completed spatial configurations, not the act of formation itself.

In compound structures such as 3D + T, the speed of light is not merely a ratio of distance to time but a dimensionless constant determined by the ratio of inner (real) to outer (imaginary) time. Because observers are subject to a temporal delay�the finite time required for spatial re-creation�they perceive a finite and invariant speed, a delay that scales with the system�s dimensional complexity.

Thus, the constancy of the speed of light is not an empirical artifact but a direct consequence of the orthogonal structure of complex-time geometry. It marks the boundary between dynamic re-creation and physical motion, embedding the fundamental geometry of time within the observable universe.

5.2          Deriving the Fundamental Invariance from Temporal Symmetry

A pivotal consequence of DTT framework is that all frames of reference�whether inertial or non-inertial�are effectively stationary with respect to the imaginary (outer) level of time. This insight dissolves the conventional distinction between inertial and accelerated frames, thereby subsuming both the second postulate of Special Relativity (the invariance of physical laws in inertial frames) and the equivalence principle foundational to General Relativity�which will be discussed with more details in Section 6.3. Within DTT, these principles arise naturally from the underlying complex-time geometry, as will be demonstrated in Sections 6.1 and 6.3.

Additionally, Section 6.2 will show that the discrete, genuinely-complex structure of space-time enables the derivation of the mass�energy equivalence relation, E = mc², from first principles�an accomplishment that remains unattained in conventional theoretical frameworks. This background-independent symmetry is conceptually aligned with emerging approaches such as postquantum-classical gravity, which seek to preserve classical spacetime structures while integrating quantum matter dynamics [66].

5.3          The Pseudo-Riemannian Limit of DTT Discrete Symmetry

The DTT posits a fundamentally discrete structure underlying the apparent continuity of space-time. At its core is a dynamic process of re-creation: spatial geometry is perpetually generated along the inner (real) level of time, while observable evolution unfolds along the outer (imaginary) temporal axis. Although this re-creation occurs in discrete instants, the statistical aggregation of these events yields an emergent continuum�recovering, in the appropriate limit, the smooth, differentiable manifold described by General Relativity.

In this continuum limit, the discrete symmetry intrinsic to DTT manifests as an effective pseudo-Riemannian geometry. The Lorentzian signature of space-time, characterized by a non-Euclidean metric tensor g_�ν with signature (−,+,+,+), emerges as a macroscopic approximation of the underlying granular dynamics of complex-time. Specifically, the instantaneous re-creation of geometrical points at the inner level is imperceptible to physical observers�who themselves are subject to re-creation�thereby giving rise to the illusion of continuous coexistence and smooth propagation.

Mathematically, the transition from the discrete complex-time manifold to a pseudoRiemannian manifold can be understood through a coarse-graining procedure. In the high-density limit of re-creation events, the temporal granularity becomes negligible relative to observational resolution, and the smooth metric structure emerges from the averaged behavior of discrete transitions:

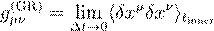�������������������������������������������������������������������������� ,������������������������������������ (5)

where δx^� represent discrete geometrical displacements generated at each inner-time instant. This limit formalizes the correspondence principle within DTT: General Relativity is retrieved as an effective theory when the dynamic formation of dimensions is not resolved.

The pseudo-Riemannian limit of DTT encodes a profound duality: the geometry of space-time is not fundamental but emergent, arising from a deeper metaphysical dynamics. General Relativity remains an excellent large-scale approximation, but its smooth manifold structure conceals the discrete and sequential fabric of reality governed by the Duality of Time.

Following the correspondence principle, any new theory must recover established frameworks under appropriate limiting conditions. Just as classical mechanics emerges from special relativity in the low-velocity limit, and special relativity itself is recovered from general relativity in the absence of gravitational fields, so too does general relativity emerge as an effective approximation of the Duality of Time Theory when the inner levels of time are neglected�as is implicitly assumed in conventional approaches.

Conventional physics assumes that all spatial points and physical objects coexist continuously in time, thereby reinforcing the illusion of continuity. This assumption underlies the use of differential calculus to model motion, where velocity is computed as the rate of continuous displacement: v = dS/dt. By contrast, DTT framework reinterprets velocity not as continuous displacement, but as a discrete progression through outward (imaginary) time, while space itself is internally and sequentially re-created along the inward (real) levels of time, which we do not directly perceive.

Consequently, the instantaneous velocity is strictly zero at every instant of normal time; what appears as continuous motion is, in fact, a statistical average over a sequence of discrete configurations, as illustrated in Figure 1. This fundamental reinterpretation of motion not only resolves longstanding paradoxes in general relativity�such as those involving singularities and infinite densities�but also provides a natural bridge to the quantum domain, where discreteness is a defining feature of physical reality.

In addition to providing a unified metaphysical and mathematical framework for space-time emergence, the genuinely-complex time-time geometry presented here invites empirical exploration. Potential signatures of the underlying discrete dynamics could include subtle anomalies in gravitational wave propagation, cosmic background isotropy, or high-energy scattering phenomena. Future work will focus on formalizing these predictions to facilitate observational testing and further integration with quantum gravity phenomenology.

In the continuum limit, where the inner temporal dynamics become observationally negligible, the discrete structure of complex-time geometry statistically converges to a smooth pseudo-Riemannian manifold, thereby recovering the classical framework of General Relativity. The Lorentzian metric signature, the principle of equivalence, and the geodesic motion of free particles naturally emerge from the underlying re-creation dynamics when coarse-grained over sufficiently large temporal and spatial scales. Thus, DTT not only provides a deeper ontological origin for space-time geometry but also satisfies the correspondence principle by reducing to General Relativity under appropriate limiting conditions. This establishes DTT as a viable and rigorous extension of gravitational theory, capable of unifying discrete quantum structures with continuous classical spacetime.

6           Mathematical Formulation of Complex�Time Geometry

In this Section, we develop a rigorous mathematical formulation of the genuinely-complex time-time geometry introduced in Section 4.2. This novel framework offers a discrete, background-independent foundation for the emergence of space-time structure, from which the mathematical formulation of relativity�including the mass�energy equivalence�naturally arises.

Recognizing that space is internally re-created at the sole real speed c, while the apparent velocity v of physical objects emerges along the outer (imaginary) time, leads directly to a reformulation of Lorentz transformations within the hyperbolic split-complex space. In this framework, not only velocity but also momentum and energy become complex-valued quantities, maintaining invariance under transformations between inertial and non-inertial frames alike.

In all cases, the instantaneous velocity in this discrete geometry is strictly zero, as motion is replaced by successive re-creation�regardless of whether the object appears at rest, moves uniformly, or accelerates. Consequently, the invariance of physical laws and the equivalence principle are not postulates but direct consequences of the underlying complex-temporal structure, as elaborated in Section 5.

Furthermore, DTT framework enables an exact derivation of the mass�energy or relativistic energy-momentum relation from first principles, without relying on approximations or heuristic arguments. This derivation simultaneously provides a unified explanation of gravitational and inertial mass, both emerging from the discrete and dynamic nature of space-time at its most fundamental level.

While several results formally resemble those of Special Relativity, they originate here from a fundamentally different ontological basis: the intrinsic discreteness of space revealed through the dynamic formation of dimensions. Beyond recovering established relativistic outcomes, this approach opens new avenues for derivations and physical insights that remain inaccessible within the standard continuous space-time paradigm.

6.1          Deriving Lorentz Transformations

Poincar�e originally showed that Lorentz transformations can be interpreted as rotations in a space-time plane using imaginary time [40]. For instance, consider the space-time coordinate X = ct + jx in one frame. In another frame moving at constant velocity v < c, the transformed coordinate is: X^′ = Xe^−jϕ = (ct + jx)(coshϕ + j sinhϕ), where

tanhϕ = v/c = β, and γ = coshϕ = 1/^p1 − v²/c².

In the DoT framework, time�not space�is represented by the complex coordinate T = t_r + jt_i = (x/c) + jt_i, where t_r is the real part (inner-time that generates space), and t_i is the imaginary part (outer-time). Thus, the Lorentz transformation becomes a rotation in the complex-time plane: T ^′ = Te^−jϕ = (t_r + jt_i)(coshϕ + j sinhϕ).

In this context, the speed of light c represents the real, intrinsic �rest speed� of recreation in the inner-time, while v is the imaginary, apparent velocity in the outer-time.

������������� Hence, the complex velocity is given by: V = c + jv,�� with β = v/c = tanhϕ and γ =

.

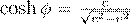As illustrated in Figure 2, this construction emphasizes that apparent motion in any direction interrupts the real inner-time flow that continuously re-creates space. Therefore,√

������������ the actual velocity of any point in the system is always less than c: v_a =����� c² − v².

This also implies that all objects are intrinsically moving at the speed of light in the inner real time, even when they appear stationary or slow-moving from the outer (imaginary) time perspective. Their apparent velocity is simply the projection of this real motion onto the imaginary axis, which decreases as v increases, but the total magnitude in complex-time remains bounded by c.

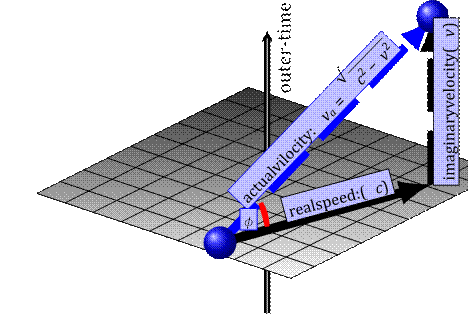
Figure 2: The actual velocity v_a is the modulus of split-complex velocity that combines the real speed√ v_r = c with the imaginary velocity v_i = v, thus: v_a = ∥v_c∥ = ∥v_r + jv_i∥ = ∥c + jv∥ =√ c² − v², from which we can easily calculate Lorentz factor as γ = c/v_a =

��������� coshϕ = c/�������� c² − v² = 1/^p1 − v²/c².

The Lorentz factor is therefore the ratio of the real velocity c to the actual velocity v_a, which is equal to coshϕ, as illustrated in Figure 2:

������������������������������������������������������ )��������������� (6)

6.2          The Mass�Energy Equivalence Relation

Beyond elucidating the constancy and invariance of the speed of light�and unifying it with the second and third principles of Relativity�the DTT introduces a fundamentally distinct framework in which the equivalence and mutual convertibility between mass and energy (E = mc²) emerge naturally. In contrast to conventional relativity, where mass�energy equivalence is introduced heuristically and derived approximately, within the DoT framework it arises directly from the underlying structure of complex-time� a process achievable only through the dynamics of the inner temporal levels, without invoking supplementary postulates or approximations.

Although E = mc² is central to modern physics, its original theoretical foundation remains incomplete. While certain heuristic arguments�such as dimensional analysis or field-theoretic analogies in electromagnetism�can suggest a relation of the form E ∝ mc², these are not derivations in the rigorous sense. Einstein�s 1905 derivation [67], invoking the Doppler effect and Maxwell�s theory of radiation, was soon challenged by Planck [68] and ultimately shown to be flawed by Ives [69]. Einstein himself acknowledged the inadequacy of his argument in 1907 [70] and made multiple subsequent attempts to derive the formula, each compromised by hidden assumptions or approximations [71].

In a 1955 letter to Carl Seelig, Einstein admitted: �I had already previously found that Maxwell�s theory did not account for the micro-structure of radiation and could therefore have no general validity� [72]. Subsequent treatments, such as Rohrlich�s 1990 derivation [73], similarly relied on significant approximations. Thus, despite its empirical success, no universally accepted exact derivation of E = mc² has been achieved within conventional frameworks.

By contrast, the DoT framework derives mass�energy equivalence from first principles, without recourse to approximations or external assumptions. As illustrated in Figure 3, the transmutation between mass and energy occurs exclusively within the inner levels of time, where motion at the speed of light appears instantaneous relative to the outer (observable) level. This sharply departs from conventional relativity, wherein such mo-

tion would imply an infinite Lorentz factor γ = 1/^p1 − v²/c² and consequently infinite mass and energy. Within the DoT structure, however, this transition remains physically permissible because the constituent geometrical points are intrinsically massless; their continuous coupling and decoupling processes generate mass and energy emergently across distinct temporal layers�a mechanism entirely absent in traditional models.

As detailed in Section 4.2, the limited apparent velocities of massive objects in DTT emerge from the spatiotemporal superposition of dual-state velocities of their massless constituent points. Whereas relativity treats mass and motion as smooth, continuous properties of spacetime, DTT reveals that each geometrical point either remains stationary or moves at the intrinsic speed of creation within the inner temporal flow. The collective dynamics of these points give rise to the observed finite mass m, energy E, and apparent velocity v, all computable using Equation 2 in Section 4.3. Furthermore, while General Relativity recovers Lorentz transformations by postulating the invariance of physical laws, DTT derives these transformations directly from the discrete symmetry inherent in complex-time geometry, thereby obviating the need for external postulates.

Accordingly, in DTT, the mass�energy equivalence arises not as an empirical observation but as a direct mathematical consequence of dual-state velocity, corresponding to a square integral in Figure 3 associated with an abrupt velocity shift from v = 0 to v = c. In contrast, interpreting v as continuous�as in classical mechanics�produces a triangular integral, leading to the conventional kinetic energy expression.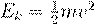

Building on this intrinsic behavior of inner-time, we will present several exact derivations of mass�energy equivalence, beginning from the classical definition of mechanical work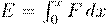. The first two derivations, detailed in Sections 6.2.2 and 6.2.3, involve integration over the inner-time, assuming either an abrupt velocity transition from 0 to c, or a mass-generation process from 0 to m, respectively�both scenarios inaccessible under the normal-time dynamics assumed by conventional physics.

A third derivation, outlined in Section 6.2.7, yields the full relativistic energy expression 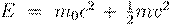�by integrating across both the inner and outer temporal layers, thereby providing a unified perspective that surpasses standard relativistic treatments. Section 6.2.8 further derives the relativistic energy�momentum relation E² = (m₀c²)² + (pc)² from first principles, again integrating across the dual temporal structure and accounting for the discrete formation of space-time at each level.

Moreover, unlike conventional treatments wherein the arrow of time and entropy increase are imposed externally onto spacetime dynamics, DTT embeds a natural arrow of time within its complex-temporal geometry, intrinsically breaking classical time-reversal symmetry and generalizing the entropic decoherence mechanisms proposed in quantum foundations [74].

Finally, Sections 6.3 and 7.5 demonstrate that the invariance�not merely the covariance� of complex momentum and energy leads to additional exact derivations of mass�energy

equivalence, recovering m = γm₀ and E = ^p(m₀c²)² + (pc)² directly from the dualtemporal structure without invoking supplementary assumptions. Additionally, since the new vacuum state (c,0) behaves as a perfect superfluid, an alternative derivation based on wave propagation yields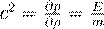, although this method will not be further pursued in the present article.

6.2.1        The Classical Kinetic Energy (in Normal Time)

In classical mechanics, kinetic energy is defined as the work done in accelerating a particle over an infinitesimal time interval dt. This work is given by the dot product of the applied force F and the resulting displacement dx:

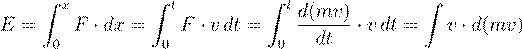������������������������������������ ,�������������������������������������������������������������������������������������������������� (7)

which leads to:

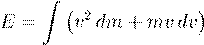��������������������������������������������������������������������������� �.������������������������������������� (8)

Now, assuming constant mass m (i.e., dm = 0; the treatment of relativistic mass will be addressed in Section 6.2.4), the expression reduces to:

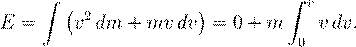����������������������������������������������������������� ����������������� (9)

Hence, within the classical framework of apparently continuous existence�where both space and time are treated as real and smoothly varying�this infinitesimal and continuous change in velocity from 0 to v yields the standard expression for the kinetic energy of a massive particle or object moving within the normal level of time:

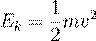����������������������������������������������������������������������������������������� .������������������������������������������������ (10)

The presence of the factor �in this equation arises from the gradual increase in velocity over time, which causes the integral to correspond to the area under a straightline velocity-time graph�specifically, the area of a triangle�as illustrated by the first arrow in Figure 3.

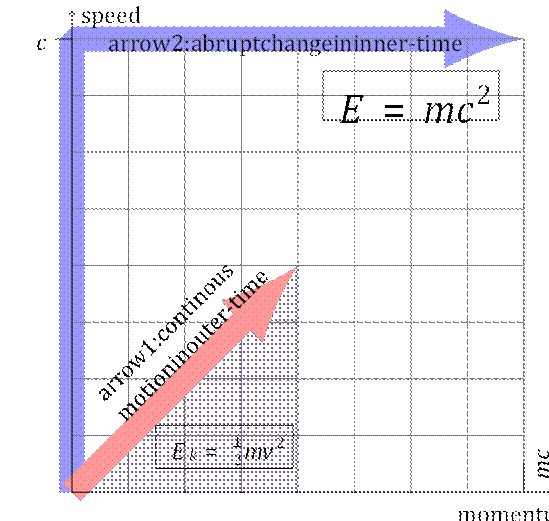
Figure 3: Schematic illustration of the integration profiles corresponding to energy acquisition. In the classical case (arrow 1), the gradual acceleration from rest to velocity v yields a triangular area, corresponding to the kinetic energy 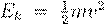. In the DoT framework (arrow 2), the abrupt transition between two discrete states�void and vacuum�at the inner level of time yields a rectangular area, corresponding directly to the mass�energy equivalence E = mc².

6.2.2        Method I (Abrupt Change of Speed in the Inner Time)

The relativistic energy�momentum relation will be derived in Section 6.2.8, but the simple mass�energy equivalence relation, E = mc² (without the �half� factor), can be obtained directly from the same integration in Equation 9 if and only if we assume that an object of mass m transitions from rest to c, or vice versa, in zero time. This situation, however, contradicts the conventional laws of motion, as such an instantaneous transition would imply infinite acceleration�and thus infinite force and energy. Nonetheless, light exhibits such behavior in processes like pair production or photon emission and absorption; however, photons are massless and thus do not experience inertia or acceleration in the conventional sense.

With the introduction of the DoT framework and the associated concept of perpetual re-creation, this issue is naturally resolved. In this model, the conversion between mass and energy occurs sequentially within the inner levels of time, at the scale of massless geometrical points that constitute the particle. The entire process appears as a single instantaneous event from the perspective of the outer (observable) level, as illustrated in Figure 1.

Thus, integrating Equation 9 directly from 0 to c�effectively summing over only two states: void and vacuum�and noting that dm = 0 (since the apparent mass does not change in this process), yields:

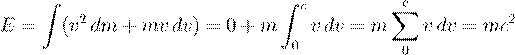������������������������������������� .������������������������������������������������������������������������������������������������� (11)

The distinction between this result and the classical kinetic energy case, shown in Equation 10, is illustrated in Figure 3. In the classical case, the integration yields the kinetic energy E_k as the area under a triangular profile (arrow 1), whereas in the present case it corresponds to the area under a rectangular profile (arrow 2).

6.2.3        Method II (Generating Mass in the Inner Time)

As discussed in Section 4.6, DTT framework provides a fundamental mechanism for mass generation within a superfluid vacuum, wherein mass arises through interaction with the dynamic structure of this physical vacuum. The mass�energy equivalence can be derived directly from Equation 8 by considering a sudden decoupling of the geometrical points constituting a particle. This process occurs within the inner levels of time and appears instantaneous from the perspective of the outer (observable) level. Assuming dv = 0 and v = c, and integrating over the mass from 0 to m, we obtain:

��������������������������������������������������������� Z������������������������������������������������ Z ^m

����������������������������������������������� E =�������� (v² dm + mv dv) = c^{2�����������������} dm + mv(0) = mc².����� (12)

0

Unlike the classical case in Equation 10, where speed changes continuously over normal time, the results in Equations 11 and 12 critically rely on the discrete inner-time dynamics, where such instantaneous transformations are physically permissible.

This mechanism resonates with analogies drawn from superfluid vacuum models in cosmology, including recent reconstructions of gravitational dynamics using unified dark fluid models [75].

6.2.4        Note I (Relativistic Mass)

If mass is treated as variable with speed, as in early formulations of Special Relativity, one

distinguishes between rest mass m₀ and relativistic mass m = γm₀ = m₀/^p1 − v²/c². Deriving the mass�energy equivalence E = m₀c² from this relation would require computing dm/dv, which is nonzero and therefore modifies the assumptions underlying Equation 9. However, since the relation m = γm₀ is itself derived assuming the equivalence E = m₀c², this approach leads to a circular argument. Thus, the two relations are mathematically equivalent and cannot be treated as independent derivations.

6.2.5        Note II (Mass-Energy Duality)

At the fundamental level, an entity exists either as massless energy�a wave propagating at the speed of creation within the inner-time�or as passive mass�a particle at rest within the outer-time. All observable phenomena emerge from superpositions of these two primordial states. Within any closed system, such as a particle or an atom, continuous fluctuation occurs between void (v_i = 0) and vacuum (v_r = c), resulting in an indeterminate state until a measurement is performed.

Thus, the entire Universe perpetually oscillates between particle-like and wave-like configurations, succinctly expressed by the equivalence:

m₀c² ⇌ hf

A particle at rest can be excited into a wave, and a wave can collapse into a particle. Although these two states cannot coexist simultaneously at the primary level of time, their superpositions generate all dynamic interactions and motion observed on the macroscopic level.

6.2.6        Note III (Effective Mass)

Even as an object approaches a velocity near c, its instantaneous velocity at the moment of measurement remains v_i = 0, and its mass remains the rest mass m₀. The kinetic energy in this case is given by:

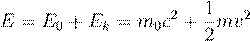���������������������������������������������������������������������� ,���������������������������� (13)

where E₀ is the rest energy and E_k is the kinetic energy associated with motion.

The total relativistic energy, expressed using the Lorentz factor γ = 1/^p1 − v²/c², becomes:

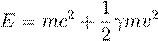���������������������������������������������������������������������������������� .���������������������������������������� (14)

Thus, mass should always be interpreted as the invariant rest mass m₀, while energy is relativistic in nature, encompassing both rest and kinetic contributions depending on the object�s apparent velocity.

6.2.7        Method III (Total Relativistic Energy)

The total relativistic energy in Equation 13 can also be derived by integrating Equation 8 across both the inner and outer levels of time. In the inner level, the rest energy E₀ = m₀c² is generated through the processes dv = c and dm = m₀, while in the outer level, the kinetic energy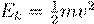 accumulates as the rest mass m₀ acquires an apparent velocity v. The full integration can be expressed as:

���������������������������������������������� �� (15)

Evaluating these integrals yields:

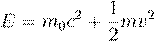���������������������������������������������������������������������������������� .����������������������������������������� (16)

More generally, the total relativistic energy can be written in the standard energy� momentum form:

����������������������������������������������������������� E = ^p(m₀c²)² + (pc)²,�������� where����� p = γm₀v.�������������� (17)

6.2.8        Method IV (Complex Momentum and Energy-Momentum Relation)

Using the definition p = mv, and accounting for the metaphysical generation of mass within the inner-time along with motion in the outer-time, we define the complex momentum p_c as:

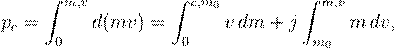������������������������������������������������������ ���������� (18)

where j denotes the imaginary unit associated with the orthogonality between inner and outer temporal levels. Evaluating the integrals yields:

������������������������������������������������� p_r = m₀c,�������� p_i = γm₀v,������� thus������� p_c = m₀c + jγm₀v.

The magnitude of the complex momentum is:

���������������������������������������������������������������������������� ∥p_c∥ = ^p(m₀c)² − (γm₀v)².���������������������������������� (19)

Multiplying by c gives the corresponding energy:

���������������������������������������������������� E = c∥p_c∥ = ^p(m₀c²)² − (pc)²,��������� with����� p = γm₀v.������� (20)

This expression, characterized by a negative contribution from the imaginary component, reflects the complex nature of time and energy, and leads naturally to a hyperbolic� rather than Euclidean�structure of spacetime, a key prediction of DTT framework. For further implications, see Sections 6.3 and 7.5.

6.3          The Equivalence Principle of General Relativity

In progressing from Special to General Relativity, Einstein observed the equivalence between the gravitational force and the inertial force experienced by an observer in a non-inertial frame of reference. This principle is closely related to the equivalence between active gravitational mass and passive inertial mass, which has since been confirmed with high precision through numerous experiments [76,77]. However, there is no direct mathematical derivation of the equivalence principle; it is primarily supported through Einstein�s famous thought experiment involving a spacecraft and an accelerating frame, which relies on inductive reasoning rather than deductive proof.

By combining this equivalence principle with the two postulates of Special Relativity, Einstein was able to predict the curved geometry of spacetime, leading to the formulation of the Einstein field equations�a system of partial differential equations relating spacetime curvature to the energy and momentum of matter and radiation.

As explained in Section 6.2, an exact derivation of the mass�energy equivalence relation is not possible without postulating the inner levels of time. For the same underlying reason, there is likewise no purely mathematical derivation of the equivalence principle that connects gravitation with geometry.

Due to the discrete structure of the complex-time geometry, as illustrated in Figure 1, the complex momentum p_c must be invariant across both inertial and non-inertial frames, because, effectively, all objects are always at rest in the outer level of time, as discussed in Section 4. Consequently, complex momentum remains conserved even when the velocity changes, i.e., as an object accelerates between different non-inertial frames.

This invariance is conceptually understandable: as an object�s velocity increases, the gain in kinetic momentum p_i = mv (the imaginary component) is precisely compensated by an increase in the effective mass m = γm₀, which simultaneously enhances the real component p_r = mc. Since the complex momentum p_c = p_r +jp_i has a hyperbolic struc-

ture, its modulus ∥p_c∥ = ^p(mc)² − (mv)² remains invariant. This inherent balancing mechanism renders the geometry of space (manifested through mc) dynamic, since space must respond to changes in effective mass in order to maintain momentum conservation.

Therefore, a physical system is truly closed only when it includes not merely the mass and energy of its contents (including kinetic and radiation contributions), but also the background space itself, corresponding to the vacuum state (c,0). In such a complete system, the complex momentum is either p_r = mc for entities re-created within the inner levels, or p_i = mv for objects moving in the normal outer level of time. Accordingly, the total complex momentum p_c = p_r + jp_i remains absolutely invariant.

In fact, without this exotic invariance of complex momentum, it would be impossible to derive the exact relation m = γm₀, which, as previously discussed in Section 6.2, is mathematically equivalent to E = m₀c². These experimentally verified relations hold true if and only if the modulus ∥p_c∥ remains conserved throughout dynamical evolution. For instance, when an object accelerates from rest to a velocity v, leading to the transformation of its effective mass from m₀ to m, the conservation of ∥p_c∥ ensures the validity of the relation:

√

����������������������� ^p(mc)² − (mv)² = ^p(m₀c)² − (m₀ � 0)² = m₀c ⇒ m = m₀c/������� c² − v² = γm₀.��������������������������������������������������������������������������� (21)

Therefore, in addition to the previous methods presented in Equations 11 and 12, and the relativistic energy�momentum relation in Equation 20, the mass�energy equivalence relation E = m₀c² can now also be deduced from Equation 21. As discussed in Section 6.2.4, the relations E = m₀c² and m = γm₀ are mathematically equivalent: deriving one necessarily leads to the other. Yet, no exact derivation of either form exists within the current formulation of Relativity.

This absolute conservation of complex momentum under acceleration leads directly to the equivalence between active and passive masses. Specifically, the total (complex) force F_c = dp_c/dt must have two components: one associated with acceleration as v changes in the outer-time t_i, corresponding to the imaginary part of the force, and another associated with the change in effective mass m = γm₀, manifested as the deformation of space being continually re-created in the inner-time t_r.

The first component, corresponding to the imaginary force F_i = ma = mdv/dt, relates to the passive mass. The second component, related to the real force F_r, arises from changes in m = γm₀ (or equivalently, E = mc²) and is associated with the gravitational force generated by the active mass. For the conservation of total complex momentum, these two components must be equivalent. Thus, gravitation emerges as a reaction to the disturbance of space from its ground-state bosonic vacuum (c,0) toward the fermionic particle state (c,v): the former linked to active mass in the real momentum mc, and the latter to passive mass in the imaginary momentum mv.

However, due to the fractal structure of the genuinely-complex discrete space�time geometry, differentiating the complex function p_c = mc + jmv requires non-standard analysis, since the underlying spacetime is no longer everywhere differentiable [78]. A rigorous treatment of this differentiation lies beyond the scope of the present article and will be addressed in future work.

6.4                 Deriving the Einstein Field Equations from the DoT Postulate

We have seen in ???? DTT derives physical complexity from metaphysical unity, making differential equations emergent�not fundamental.

From the conservation of complex momentum, one should in principle be able to derive the law of gravitation and the form of the stress�energy�momentum tensor leading to the Einstein field equations. Furthermore, since empty space is now described as a dynamic aether, gravitational waves correspond to longitudinal vibrations within this ideal medium, while the graviton may be interpreted as the moment of time mv�analogous to how photons, as the quanta of electromagnetic radiation, represent moments of space mc in the transverse vibrations of the vacuum.

This perspective suggests that the equivalence principle is fundamentally an equivalence between photons and gravitons�or, more generally, between space and time�with electrons and other fermionic particles appearing as standing waves within the complexified space�time structure, characterized by complex momentum mc + jmv. Moreover, the existence of three generations of fermions may be directly related to the three spatial dimensions.

This important conclusion warrants further investigation. However, it should be noted here that the equivalence principle may apply universally to all fundamental interactions, not only to gravity, since it reflects a deeper property of space�time geometry at all dimensions, and not merely the three spatial dimensions where gravity predominantly manifests, as discussed further in [79].

��- In standard General Relativity, the Einstein Field Equations (EFE) relate the curvature of spacetime to the distribution of mass-energy:

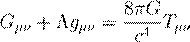������������������������������������������������������������������������������ ,������������������������������������ (22)

where G_�ν is the Einstein tensor, T_�ν is the stress-energy tensor, Λ is the cosmological constant, G is Newton�s gravitational constant, and c is the speed of light.

In DTT, spacetime geometry emerges dynamically from the sequential re-creation of spatial frames driven by a real inner flow of time (t_r), while the outer (imaginary) time (t_i) produces the external experience of continuity. The metric inherits a Lorentzian signature from the complex-time structure: 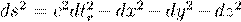, at each instant t_r, accumulating continuously along imaginary time t_i. Energy�momentum emerges as local modifications in the re-creation rate. Thus, curvature R_�ν geometrically encodes the cumulative delays induced by energy distributions: R_�ν ∝ T_�ν. Let us introduce:

Φ(x^�): Scalar field representing the local rate of real-time flow at spacetime point x^�. g_�ν: Emergent metric induced by sequential re-creation of spatial frames.

Perturbations in Φ correspond to deviations from flat spacetime, with second derivatives ∇_�∇_νΦ describing local curvature effects.

Thus, the analogous Einstein Field Equation in DTT is proposed as:

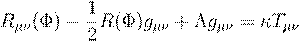���������������������������������������������������������������� ,���������������������� (23)

where κ is the coupling constant, and the curvature tensors R_�ν(Φ) and R(Φ) emerge from perturbations of the scalar re-creation field Φ. Explicitly:

g_�ν: Cumulative sequential re-creation metric.

R_�ν(Φ): Effective Ricci tensor reflecting deviations in sequential re-creation.

T_�ν: Stress-energy modifying local sequential re-creation rates.

Λ: Intrinsic vacuum energy linked to underlying sequential dynamics.

Identifying the coupling constant by matching to Newtonian limits gives:.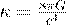

The Universe unfolds as sequential discrete spatial frames along the imaginary level of time (t_i), each frame dynamically generated through the inner real-time flow (t_r). Spacetime is therefore a dynamically emergent structure. To ensure energy�momentum conservation, the contracted Bianchi identity 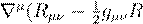) = 0 imposes a generalization:

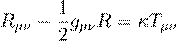������������������������������������������������������������������������������� .�������������������������������������� (24)

Including intrinsic vacuum tension, the cosmological constant Λ arises naturally, yielding the full DTT field equations:

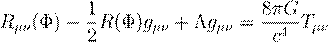������������������������������������������������������������ .������������������� (25)

The EFE thus emerge naturally from the dual-time ontology, bridging metaphysical principles and empirical gravitation phenomenology. The following table summarizes the main advantages introduced by DTT:

Aspect	General Relativity	Duality of Time Theory
Space-time	Pre-existing manifold	Emergent dynamic structure
Curvature	Geometric deformation	Delay in sequential re-creation
Gravity	Geometrized mass-energy	Sequential deformation dynamics
Field Equations	Covariant postulate	Emergent from internal dynamics
Cosmological Constant	Added ad hoc	Intrinsic vacuum tension

Table 2: Comparative summary of the emergence of Einstein Field Equations in General Relativity and Duality of Time Theory.

7           Emergence of Einstein Field Equations from InnerTime Dynamics

In this section, we demonstrate that the Einstein Field Equations (EFE) naturally emerge from the statistical coarse-graining of the discrete, sequential re-creation of spatial geometry in DTT.

7.1          Statistical Structure of Emergent Geometry

Let δx^� represent the microscopic re-creation displacement at each inner-time step. The macroscopic metric g_�ν emerges as the statistical average over many such re-creation events:

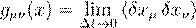����������������������������������������������������������������������������� .����������������������������������� (26)

This average defines the effective smooth pseudo-Riemannian manifold perceived at macroscopic scales.

7.2          Stress-Energy Tensor from Re-Creation Fluctuations

Define the microscopic momentum fluctuations as δp_�, with the associated fluctuation tensor:

������������������������������������������������������������������������������������ Π_�ν(x) = ⟨δp_� δp_ν⟩.����������������������������������������� (27)

Since momentum is tied to re-creation displacements via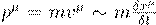, the stressenergy tensor is directly related to the variance of the re-creation process:

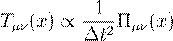�������������������������������������������������������������������������������� .�������������������������������������� (28)

Thus, local energy and momentum densities emerge as manifestations of statistical fluctuations in the microscopic re-creation dynamics.

7.3          Emergent Curvature from Re-Creation Inhomogeneities

In regions of uniform re-creation, space remains flat. Curvature arises from variations in the re-creation rates across neighboring points. The emergent Riemann curvature tensor is built from gradients of the statistical connection coefficients Γ^λ_�ν:

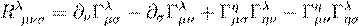��������������������������������������������������������� .��������������� (29)

The Ricci tensor and scalar are then defined in the standard way:

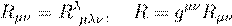������������������������������������������������������������������������ .������������������������������� (30)

7.4          Emergent Einstein Field Equations

Since both stress-energy and curvature originate from statistical properties of the recreation process, a proportionality between them naturally arises. At macroscopic scales, this yields the Einstein Field Equations:

������������������������������������������������������������������������������������� G_�ν + Λg_�ν = κT_�ν,������������������������������������������ (31)

where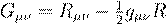is the Einstein tensor, Λ represents the cosmological constant associated with the mean background energy of the re-creation vacuum, and .

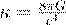Thus, the Einstein Field Equations emerge naturally as the macroscopic statistical law governing the relationship between curvature (inhomogeneities in re-creation) and stressenergy (fluctuations in the re-creation dynamics) within the genuinely-complex time-time geometry of DTT.

7.5          Complex Energy and the Fundamental Atomic Interactions

Since energy is intimately tied to time, it must likewise possess a complex structure, involving multiple intersecting dimensions in accordance with the spatial and material dimensions generated at the inner levels of time before evolving outward into the outer level. It is important to note, however, that not all these energy levels are equivalent to mass, which is specifically a property of 3-dimensional space. In lower dimensions, energy is instead associated with the corresponding coupling properties, such as electric or color charges. Consequently, it is expected that negative mass is possible only in 4 spatial dimensions, as previously anticipated in the literature [80,81].

It becomes immediately clear�just as we observed for time, velocity and momentum� that when the complex nature of time is taken into account, the kinetic energy 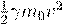in Equation 13, or pc in the relativistic energy-momentum relation 17, becomes negative relative to the potential energy mc² stored in the rest mass m. Therefore, the total energy E in Equation 15 becomes a complex quantity E_c with distinct real and imaginary parts, E_r and E_i respectively. Specifically, the real part E_r corresponds to the re-creation process through changes in mass dm, while the imaginary part E_i reflects the kinetic evolution of mass through changes in the apparent velocity dv:

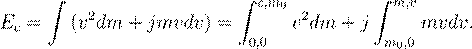�������������������������������������������� (32)

Thus, the real part is E_r = m₀c², while the imaginary part is E_i = γm₀vc = pc, leading to the modulus:

���������������������������������������������� ∥E_c∥ = ^p(m₀c²)² − (γm₀vc)² = ^p(m₀c²)² − (pc)²;p = γm₀v.��� (33)

The negative contribution of the kinetic term does not invalidate Equations 13 and 17; rather, it signifies that potential and kinetic energies belong to orthogonal levels of time. The conversion between potential and kinetic energy mirrors the transition from inner to outer levels of time. Once both components are projected into the outer (imaginary) time, they are combined additively, consistent with conventional treatments.

Moreover, as discussed in Section 6.3 for momentum, energy is absolutely conserved even when the apparent velocity v varies. This follows from the fact that the instantaneous velocity v_i in the outer level of time is always zero, as shown in Section 4 and Figure 1. Just as with momentum, the absolute conservation of energy arises because changes in the kinetic term E_i = mvc (the imaginary part) are precisely compensated by changes in the effective mass m = γm₀, thereby maintaining the real energy component E_r = mc². Since E_c = E_r + jE_i is hyperbolic, its modulus remains invariant under transformations between inertial and non-inertial frames:

���������������������������������������������������������������������� ∥E_c∥ = ^p(mc²)² − (mvc)² = m₀c².��������������������������� (34)

This expression offers an alternative derivation of the mass-energy equivalence, since the left-hand side simplifies as follows:

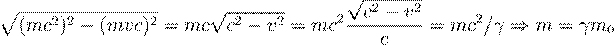������������������ .��������������������������������������������������������������������������������������������� (35)

which leads immediately to: m = γm₀.

Thus, combining Equations 34 and 35, we recover the standard mass-energy equivalence E = m₀c². Furthermore, we observe that the general expression 32 for the total complex energy E_c across the inner and outer levels of time reduces to the classical kinetic energy E_k when the complex structure of time is ignored (i.e., when dm = 0 for non-relativistic velocities).

8           Empirical Predictions and Observational Signatures

The DTT offers a novel ontological and mathematical basis for addressing persistent problems in theoretical physics and cosmology. By modeling space-time as a dynamically re-created structure emerging from inner temporal recurrence, DTT provides a reinterpretation of the vacuum structure, a reformulation of mass generation, and a proposed resolution to the cosmological constant problem. This framework yields several distinct experimental and observational predictions, as summarized below.

Recent developments in quantum gravity research increasingly emphasize the empirical detectability of spacetime�s discrete or emergent structure. Microscopic measurements of gravitational forces are now achievable, offering promising avenues to test deviations from classical relativity [82]. Proposals for tabletop experiments targeting emergent spacetime features [35] further support the view that quantum-geometrical effects could soon be within experimental reach. Observational evidence also suggests that dark energy may encode subtle imprints of quantum gravity phenomena, consistent with string-theoretic and emergent spacetime predictions [83]. Furthermore, suppression mechanisms in causal set theory [30] and background-independent Lorentzian quantum gravity models [84] demonstrate that discrete, dynamic structures can recover continuum-like behavior, aligning with the dynamical layering proposed in DTT. Together, these advances provide strong motivation for outlining potential observational signatures of the complextime geometry framework introduced here.

8.1          Potential Observational Signatures of Complex-Time Geometry

The genuinely-complex time-time structure of DTT predicts several empirical deviations from standard cosmology and general relativity. We outline key testable consequences:

1.   Gravitational Wave Dispersion: The discrete re-creation dynamics predict slight frequency-dependent dispersion of gravitational waves at cosmological scales. Deviations from Lorentz-invariant propagation could be detectable by LISA and next-generation observatories. Microscopic-scale experiments are increasingly sensitive to gravitational interactions at extremely short distances, as demonstrated by recent quantum-scale gravity measurements [82], suggesting that deviations from standard predictions could soon become observable.

2.   Cosmic Microwave Background (CMB) Anomalies: Residual imprints of early universe inner-time synchronization could manifest as low-multipole anomalies or hemispherical asymmetries in the CMB.

3.   Vacuum Decoherence Rates: The structured vacuum implies subtle deviations from perfect vacuum stability, possibly detectable as minute variations in Casimir forces or precision atom interferometry experiments.

4.   Dark Energy Evolution: A time-averaged structured vacuum suggests a slowly varying dark energy component, which could be observed through late-time cosmological surveys measuring the equation-of-state parameter w(z).

5.   Fine-Structure Constant Variability: Spatial or temporal drift in fundamental constants, such as α, could arise from differential evolution of inner vs outer time rates over cosmic history.

8.2          Quantitative Estimate: Gravitational Wave Dispersion

A key prediction of DTT framework is the emergence of subtle gravitational wave dispersion due to the discrete and dynamic structure of space-time at small scales. In particular, the sequential re-creation of geometrical nodes introduces a minuscule deviation from the exact Lorentz invariance, leading to an energy-dependent propagation speed for gravitational waves. Similar experimental motivations have driven proposals for detecting emergent spacetime features through precise quantum mechanical setups [35], highlighting the feasibility of probing minute anomalies in gravitational wave propagation.

Assuming that each geometrical re-creation event occurs with a characteristic timescale τ_c ∼ ℓ_P /c, where ℓ_P is the Planck length, the cumulative dispersion effect over a propagation distance D can be estimated by the relation:

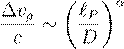��������������������������������������������������������������������������������������� ,������������������������������������������� (36)

where α depends on the dimensionality of the inner temporal structure. For a linear accumulation, α = 1, yielding

������������������������������������������������������������������������� ���� �� .

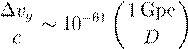
Although extremely small over astrophysical distances, such dispersion may be amplified in high-precision measurements of gravitational wave arrivals across different frequency bands, especially with next-generation detectors like the Einstein Telescope and LISA. Detecting or constraining this effect would provide a direct empirical probe of the complex-time re-creation dynamics underlying space-time.

8.3          The Physical Vacuum as Dynamic Aether

In DTT, the vacuum is not an inert backdrop but a dynamically generated medium�a superfluid-like aether arising from the recurrent re-creation of geometrical nodes in inner time. The notion of a dynamically structured vacuum aligns with emergent quantum gravity models where spacetime itself arises from underlying discrete structures [30]. Unlike historical aether concepts, this dynamic vacuum:

Is intrinsically Lorentz-invariant, as all physical motion occurs in the orthogonal outer-time.

Does not affect the speed of light, which is governed by the inner/outer temporal ratio.

Supports massless excitations, with mass emerging through temporal entanglement of geometrical nodes.

This model conceptually parallels Bose-Einstein condensate (BEC) theories of vacuum, but differs fundamentally in that space itself constitutes the ground state of the temporal condensate.

8.4          Vacuum Energy and the Cosmological Constant Problem

Standard quantum field theory predicts a vacuum energy density vastly exceeding observational data. In DTT, vacuum energy is redefined as a temporal average over sequential re-creations, rather than a summation over zero-point modes: 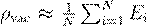, where N is the number of re-creation modes per Planck volume. This temporal averaging reduces the effective vacuum energy by at least 117 orders of magnitude, aligning with observed cosmological constant values and removing the need for fine-tuning or anthropic reasoning. Moreover, observational hints favoring string-theoretic explanations of dark energy [83] reinforce the need for alternative vacuum models, such as the dynamic temporal averaging proposed in DTT framework.

8.5          Dark Energy as a Residual Temporal Ground State

Deviations or asymmetries in the re-creation process manifest as a residual energy density, interpretable as dark energy. In DTT:

Cosmic expansion reflects the ongoing formation of space rather than a repulsive force.

Acceleration of expansion is linked to dynamic changes in local fractal dimensionality.

This predicts possible deviations from ΛCDM cosmology at high redshifts (z > 1.5), potentially observable with future surveys such as Euclid, LSST, and the Roman Telescope.

8.6          Mass Generation Without the Higgs Mechanism

Mass in DTT arises from temporal entanglement and time-lag in sequential re-creation:

Isolated geometrical points are massless.

Coupling between points via delayed re-creation induces inertia and rest mass.

The minimal number of coupled nodes defines a discrete mass spectrum, independent of spontaneous symmetry breaking.

This framework suggests possible observable consequences, such as scale-dependent neutrino mass variations and composite Higgs-like behaviors under extreme gravitational or energy conditions.

8.7          Matter�Antimatter Asymmetry and Supersymmetry Breaking

The DTT introduces two orthogonal arrows of time:

Inner (real) time generating spatial dimensions.

Outer (imaginary) time projecting observable motion and dynamics.

Matter and antimatter correspond to asymmetric projections of this dual temporal structure, providing a geometric explanation for the observed matter-antimatter asymmetry without requiring conventional CP-violation. Supersymmetry is reinterpreted as excitations along different time directions, rather than differences in particle spin alone.

8.8          Phenomenological Predictions and Experimental Signatures

The genuinely-complex, discrete temporal structure of DTT leads to several novel and potentially testable predictions:

Fractal and Scale-Dependent Spacetime: Local dimensionality depends on the inner-to-outer time ratio, possibly causing scale-dependent deviations from Lorentz invariance. Potential observational tests include gamma-ray dispersion or anomalies in ultra-high-energy cosmic ray propagation.

Temporal Origin of the Arrow of Time: The asymmetry between inner and outer time layers geometrically underpins thermodynamic irreversibility, potentially correlating with anisotropies observed in the cosmic microwave background (CMB).

Quantum Nonlocality as Temporal Synchronization: Entanglement correlations arise from synchronized re-creation across spatially separated points. Gravitational gradients might induce observable variations in entanglement decoherence times, offering new experimental probes into sub-quantum structures.

Variations in the Speed of Light: The speed of light, being the ratio of inner to outer time scales, could exhibit slight variations near singularities or at Planckscale energies. These effects might be detected through photon arrival delays from gamma-ray bursts or modified dispersion relations.

Gravitational Wave Echoes and Discrete Redshifts: Inner-time layer reflections may cause gravitational wave echoes, and discrete redshift quantization could emerge from layer-by-layer re-creation.

High-Energy Cosmic Ray Cutoff: A maximal re-creation frequency may impose a natural high-energy cutoff in cosmic ray spectra, distinct from standard GZK limits.

Vacuum Birefringence: A spin-dependent structure of the dynamic vacuum may produce vacuum birefringence, potentially detectable in experiments such as PVLAS.

Anomalous Bell Inequality Violations: Complex-time synchronization could lead to violations of standard quantum bounds (e.g., Tsirelson�s bound) in specially configured multipartite entanglement experiments.

8.9          Proposed Simulations and Experimental Tests

To guide empirical verification, several experimental or simulation avenues are proposed:

Discrete Time Quantum Field Theory Simulation Simulate field propagation on a discrete complex-time lattice to investigate emergent mass gaps, vacuum structures, and energy quantization phenomena.

Re-creative Clock Interferometry Develop ultra-stable atomic clocks sensitive to recreation frequency modulation across gravitational potentials, to test inner-time structure variations.

Neutrino Oscillation Deviations Examine potential deviations from standard neutrino oscillation patterns due to complex-time layering effects on phase accumulation.

8.10         Future Detection Channels

The empirical testability of discrete and emergent spacetime structures has gained significant momentum recently, particularly through the development of Lorentzian backgroundindependent quantum gravity models [84], and deriving massless gravitons from quantum matter interactions [85], whose spirit resonates with the complex-time dynamics described here.

Upcoming experimental facilities and observations could offer indirect evidence of the complex-time dynamics:

Space-based Observatories: LISA, Euclid, and Roman Telescope may detect gravitational wave echoes, deviations in cosmic expansion, or discrete redshift anomalies.

Quantum Optics Experiments: Bell-type inequality tests and delayed-choice quantum eraser setups could probe synchronization effects beyond standard quantum limits.

Astrophysical Observations: Time delays in high-energy photon arrival from distant sources (e.g., GRBs) could reflect inner-time layering structures.

Vacuum Structure Probes: Casimir force measurements and vacuum birefringence studies could reveal scale-dependent deviations attributable to granular vacuum properties.

The development of quantifiable predictions along these lines remains a central goal for future work, aiming to bridge the metaphysical foundations of DTT with empirical testability.

9           Conclusion and Outlook

In this work, we have introduced the Duality of Time (DoT) framework, grounded in the Re-Creation Principle of the Single Monad Model (SMM), to reinterpret the structure of space-time, motion, and mass generation from first principles. By postulating that space is not a static manifold but a dynamically re-created structure emerging from sequential cycles of inner (real) time, we constructed a genuinely-complex space-time geometry composed of orthogonal real and imaginary temporal components.

This novel structure yields a hyperbolic space-time geometry that reduces to General Relativity in the appropriate continuum limit, while simultaneously providing a deeper ontological account of discreteness, causality, and mass-energy relations. Within this framework, we derived from first principles the four foundational pillars of Quantum

Relativity:

The constancy and invariance of the speed of light, reinterpreted as a dimensionless ratio of inner to outer time intervals.

Lorentz transformations, emerging directly from the discrete structure of complextime geometry.

The mass�energy equivalence relation, derived from inner-time dynamics without reliance on field-based mass generation mechanisms such as the Higgs field.

The equivalence principle of inertial and gravitational mass, arising naturally from the internal dynamics of re-creation.

Unlike conventional formulations, where these principles are independently postulated, here they emerge coherently from the internal temporal structure without the need for an external space-time background.

Furthermore, the reinterpretation of the vacuum as a dynamically structured medium provides a resolution to the longstanding cosmological constant problem without finetuning, and offers new insights into:

Mass generation through temporal dynamics rather than scalar fields.

Quantum nonlocality as a manifestation of synchronized re-creation cycles.

Matter�antimatter asymmetry and supersymmetry breaking as consequences of the dual-time projection mechanism.

The arrow of time as an emergent feature of sequential inner-time flow.

A granular, self-organizing vacuum structure as the physical origin of both matter and dark energy phenomena.

Beyond these conceptual contributions, the DoT framework suggests potential empirical signatures, including:

Gravitational wave dispersion effects.

Anomalies in the cosmic microwave background.

Measurable variations in vacuum energy density and particle mass generation.

Future work will focus on:

Developing a complete mathematical formalism for field dynamics within the complextime geometry.

Deriving concrete, testable predictions to distinguish the DoT framework from conventional models.

Extending the framework to early-universe cosmology, black hole thermodynamics, and the foundations of quantum gravity.

Investigating connections with quantum information theoretic approaches to spacetime emergence.

In this light, the Duality of Time Theory does not merely reinterpret existing physical principles but proposes a dynamically unified ontology, wherein space, time, mass, and motion emerge coherently from a single, absolute temporal process rooted in metaphysical unity. While still in its early stages, this framework offers a promising new pathway for unifying quantum mechanics, relativity, and cosmology, and for developing a fully testable theory of quantum gravity.

References

[1]      M. Hobson, G. Efstathiou, A. Lasenby, General Relativity:���������� An Introduction for

Physicists (Cambridge University Press, 2006), p. 187

[2]      E. Witten, Reviews of Modern Physics 93(4), 045005 (2021)

[3]      B. Zwiebach, A First Course in String Theory, 2nd edn. (Cambridge University Press, 2021)

[4]      A. Ashtekar, J. Lewandowski, Classical and Quantum Gravity 21(15), R53 (2004)

[5]      C. Rovelli, Quantum gravity (Cambridge University Press, 2004)

[6]      R.D. Sorkin, International Journal of Modern Physics D 29(14), 2042017 (2020)

[7]      D. Oriti, Classical and Quantum Gravity 27(14), 145017 (2009).��������� DOI 10.1088/ 0264-9381/27/14/145017

[8]      A. Perez, Classical and Quantum Gravity 30(14), 143001 (2013). DOI 10.1088/ 0264-9381/30/14/143001

[9]      L.B. Szabados, Foundations of Physics (2024)

[10]  M. Haj Yousef, The Single Monad Model of the Cosmos (Single Monad Academy, 2014)

[11]  M. Haj Yousef, The Duality of Time Postulate and Its Consequences on General

Relativity and Quantum Mechanics (Single Monad Academy, 2017)

[12]  A. Ashtekar, P. Singh, Classical and Quantum Gravity 38(8), 084001 (2021)

[13]  M.A. Haj Yousef, The white pearl: Names and descriptions of the single monad (2019)

[14]  M. Haj Yousef, The Concept of Time in Ibn Arabi�s Cosmology (Routledge, 2005)

[15]  M.A. Haj Yousef, Ultimate symmetry: Fractal complex-time, the incorporeal world and quantum gravity (2019)

[16]  S.W. Hawking, in Recent Developments in Gravitation: Carg`ese 1978, ed. by M. L�evy, S. Deser (Springer US, Boston, MA, 1979), pp. 145�173. DOI 10.1007/ 978-1-4613-2955-8 4

[17]  M.A. Haj Yousef, in Islamic and Christian Philosophies of Time, Vernon Series in Philosophy, ed. by S. Mitralexis (Vernon Press, Wilmington, USA, 2018), chap. 7, pp. 147�178

[18]  M. Bojowald, Reports on Progress in Physics 84(2), 026902 (2021)

[19]  M. Kumar, Quantum: Einstein, Bohr and the Great Debate About the Nature of

Reality

[20]  M.B. Green, J.H. Schwarz, E. Witten, Superstring theory (Cambridge University Press, 1987)

[21]  B. Zwiebach, A first course in string theory (Cambridge University Press, 2009)

[22]  J. Polchinski, String theory. Vol. 2: Superstring theory and beyond (Cambridge University Press, 1998)

[23]  A. Ashtekar, Classical and Quantum Gravity 38(8), 084001 (2021)

[24]  M. Bojowald, Reports on Progress in Physics 78(2), 023901 (2021)

[25]  J. Ambj�rn, J. Jurkiewicz, R. Loll, Scientific American 299(1), 42 (2008)

[26]  L. Glaser, S. Surya, Entropy 25(3), 410 (2023)

[27]  F. Dowker, Philosophical Transactions of the Royal Society A 373(2040), 20140241 (2015)

[28]  R.D. Sorkin, International Journal of Modern Physics D 29(14), 2042003 (2020)

[29]  R.D. Sorkin, Classical and Quantum Gravity 23(22), R1 (2006).��������� DOI 10.1088/ 0264-9381/23/22/S01

[30]  S. Carlip, S. Surya, arXiv preprint (2022)

[31]  S. Ryu, T. Takayanagi, Physical Review Letters 96(18), 181602 (2006). DOI 10. 1103/PhysRevLett.96.181602

[32]  M.V. Raamsdonk, General Relativity and Gravitation 42, 2323 (2010). DOI 10. 1007/s10714-010-1034-0

[33]  C. Cao, S.M. Carroll, S. Singh, Classical and Quantum Gravity 34(7), 074002 (2017). DOI 10.1088/1361-6382/aa5a1b

[34]  B. Swingle, Physical Review D 86, 065007 (2012). DOI 10.1103/PhysRevD.86. 065007

[35]  K. Hashimoto, D. Takeda, K. Tanaka, S. Yonezawa, arXiv preprint (2022)

[36]  S. Hawking, A Brief History of Time (Bantam Books, 1998), p. 157. Updated and expanded tenth anniversary edition

[37]  B.S. DeWitt, Phys. Rev. 162, 1239 (1967). DOI 10.1103/PhysRev.162.1239

[38]  M. Panine, A. Kempf, Phys. Rev. D 93, 084033 (2016). DOI 10.1103/PhysRevD.93. 084033

[39]  M. Borunda, B. Janssen, B. Bonga, Classical and Quantum Gravity 31(4), 045018 (2014). DOI 10.1088/0264-9381/31/4/045018

[40]  M.H. Poincar�e, Rendiconti del Circolo Matematico di Palermo (1884-1940) 21(1), 129 (1906). DOI 10.1007/BF03013466

[41]  A. Einstein, The Principle of Relativity; Original Papers by A. Einstein and H.

Minkowski. Translated Into English by M.N. Saha and S.N. Bose; With a

[42]  P. Fjelstad, American Journal of Physics 54(5), 416 (1986). DOI 10.1119/1.14605

[43]  N. Loizeau, D. Sels, Foundations of Physics (2024)

[44]  M.A. Haj Yousef, The Single Monad Model of the Cosmos: Ibn Arabi�s Concept of

Time and Creation (CreateSpace, Charleston, 2014)

[45]  A. MICHELSON, E. MORLEY, SPIE milestone series 28, 450 (1991)

[46]  R. Rucker, Geometry, Relativity and the Fourth Dimension. Dover Books on Mathematics

[47]  P.A.M. DIRAC, Nature 168(4282), 906 (1951). DOI 10.1038/168906a0

[48]  I. Zlatev, L. Wang, P.J. Steinhardt, Phys. Rev. Lett. 82, 896 (1999). DOI 10.1103/ PhysRevLett.82.896

[49]  B. Ratra, P.J.E. Peebles, Phys. Rev. D 37, 3406 (1988). DOI 10.1103/PhysRevD. 37.3406

[50]  R.R. Caldwell, R. Dave, P.J. Steinhardt, Phys. Rev. Lett. 80, 1582 (1998). DOI 10.1103/PhysRevLett.80.1582

[51]  A.J. Krasznahorkay, et al., Phys. Rev. Lett. 116(4), 042501 (2016). DOI 10.1103/ PhysRevLett.116.042501

[52]  in Collected Papers of L.D. Landau, ed. by D.T. HAAR (Pergamon, 1965), pp. 546 � 568. DOI https://doi.org/10.1016/B978-0-08-010586-4.50078-X

[53]  M. Gell-Mann, R.J. Oakes, B. Renner, Phys. Rev. 175, 2195 (1968). DOI 10.1103/ PhysRev.175.2195

[54]  H. Martel, P.R. Shapiro, S. Weinberg, The Astrophysical Journal 492(1), 29

[55]  V. SAHNI, A. STAROBINSKY, International Journal of Modern Physics D 09(04), 373 (2000). DOI 10.1142/S0218271800000542

[56]  A. Padilla, Classical and Quantum Gravity 32(9), 093001 (2015). DOI 10.1088/ 0264-9381/32/9/093001

[57]  S. Weinberg, Phys. Rev. D 13, 974 (1976). DOI 10.1103/PhysRevD.13.974

[58]  L. Susskind, Phys. Rev. D 20, 2619 (1979). DOI 10.1103/PhysRevD.20.2619

[59]  A.V. Avdeenkov, K.G. Zloshchastiev, Journal of Physics B: Atomic, Molecular and Optical Physics 44(19), 195303

[60]  V. Dzhunushaliev, K.G. Zloshchastiev, Central Eur. J. Phys. 11, 325 (2013). DOI 10.2478/s11534-012-0159-z

[61]  K.G. Zloshchastiev, Acta Phys. Polon. B42, 261 (2011). DOI 10.5506/APhysPolB. 42.261

[62]  A. Jaffe, Classical and Quantum Gravity 17(24), 4997 (2000).��������� DOI 10.1088/ 0264-9381/17/24/302

[63]  A. Jaffe, E. Witten. Quantum yang-mills theory, official problem description

[64]  A. Ilinska. Structural quantum gravity (2025). DOI 10.5281/zenodo.15228615

[65]  E. Hecht, American Journal of Physics 79(6), 591 (2011)

[66]  A. Grudka, et al., Foundations of Physics (2024)

[67]  A. Einstein, Ann Phys 18, 639 (1905)

[68]  M. Planck, Verh. Deutsch. Phys. Ges. 8, 136 (1906)

[69]  H.E. Ives, JOSA 42(8), 540 (1952)

[70]  A. Einstein, Annalen der Physik 327(3), 569 (1907)

[71]  Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics 40(2), 167 (2009). DOI http://dx.doi.org/10.1016/j.shpsb. 2009.03.002

[72]  M. Capria, Physics Before and After Einstein (IOS Press, 2005), p. 82

[73]  F. Rohrlich, American Journal of Physics 58(4), 348 (1990)

[74]  J. Al-Khalili, E.K. Chen, Foundations of Physics (2024)

[75]  E.A. Elkhateeb, Foundations of Physics (2024)

[76]  S. Schlamminger, K.Y. Choi, T.A. Wagner, J.H. Gundlach, E.G. Adelberger, Phys. Rev. Lett. 100, 041101 (2008). DOI 10.1103/PhysRevLett.100.041101

[77]  R.D. Reasenberg, B.R. Patla, J.D. Phillips, R. Thapa, Classical and Quantum Gravity 29(18), 184013

[78]  L. Nottale, J. Schneider, Journal of Mathematical Physics 25(5), 1296 (1984). DOI 10.1063/1.526285

[79]  M.A. Haj Yousef, DUALITY OF TIME: Complex-Time Geometry and Perpetual Creation of Space. The Single Monad Model of The Cosmos, Book 2 (CreateSpace,

Charleston, 2017)

[80]  W.B. Bonnor, General Relativity and Gravitation 21(1143), 1157 (1989)

[81]  J.P. Petit, G. D�Agostini, Modern Physics Letters A 29(34), 1450182 (2014). DOI 10.1142/S021773231450182X

[82]  T. Fuchs, et al. Quantum physics makes small leap with microscopic gravity measurement (2024). The Guardian, available at: https://www.theguardian.com/ science/2024/feb/23/quantum-physics-microscopic-gravity-discovery

[83]  S. Hur, D. Minic, T. Takeuchi, V. Jejjala, M. Kavic. First observational evidence supporting string theory (2025). LiveScience article, available at:

https://www.livescience.com/physics-mathematics/quantum-physics/

scientists-claim-to-find-first-observational-evidence-supporting-string-theory-w

[84]  E. D�Angelo, R. Ferrero, M.B. Fro�b, arXiv preprint (2025)

[85]  S.S. Lee, arXiv preprint (2022)

View publication stats